
Electrical engineers are a unique breed. Their work is mathematically demanding, and they constantly face challenging technical problems.
Math software and spreadsheets are often used to support the calculations at the core of their analyses. However, calculations aren't just a collection of isolated mathematical operations. Electrical engineers need to:
Fundamentally, calculations need to exist in a structured, managed environment.
This whitepaper examines how electrical engineers use the software Maple for calculation management, transforming what would otherwise be isolated analyses into reusable, shareable and extensible assets.
The paper starts by examining Maple's features for doing, documenting and deploying calculations. Then, several typical electrical engineering applications are discussed.
A Maple document combines live math, text, images and plots in a single document. In effect, Maple captures the inherent assumptions and thought process behind an analysis, as well as the calculations.
Fundamentally, Maple captures design intent, and turns calculations into reusable, shareable, extensible documents.
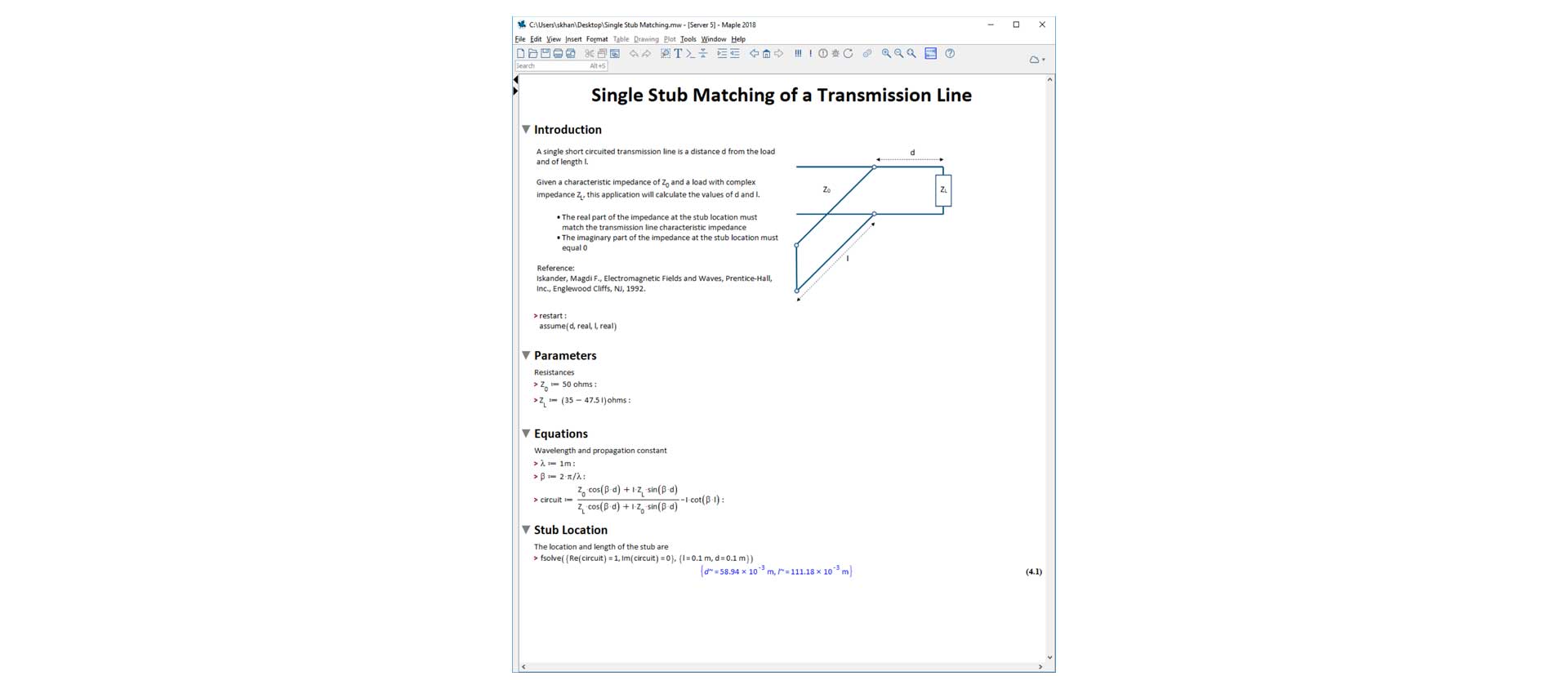
Figure 1. Document Interface
Maple offers practical high-level tools for numeric and symbolic math, data analysis, and programming. These tools are designed for both simple and complex engineering problems.
For example, Maple can solve the stiff differential equations that typically arise from analyzing electrical circuits.
The symbolic and numeric math engines are seamlessly connected; parameters, equations and calculations can fluidly flow between the two. This means you can derive and numerically evaluate your equations in a single cohesive workflow.
Moreover, Maple's programming language benefits from an interactive development environment and can use any of Maple's high-level math tools, making the code:

Figure 2. Stiff differential equation from an LRC circuit with an imposed voltage
Nearly every single quantity an electrical engineer encounters - whether it's a resistance, voltage or a length - has a unit.
Units are fluidly integrated into the Maple environment, and can be used in simple calculations as well as numeric equation solving, optimization and visualization.
Using units in calculations removes the risk of introducing unit conversion errors, and also acts as a check on the physical validity of the equations.
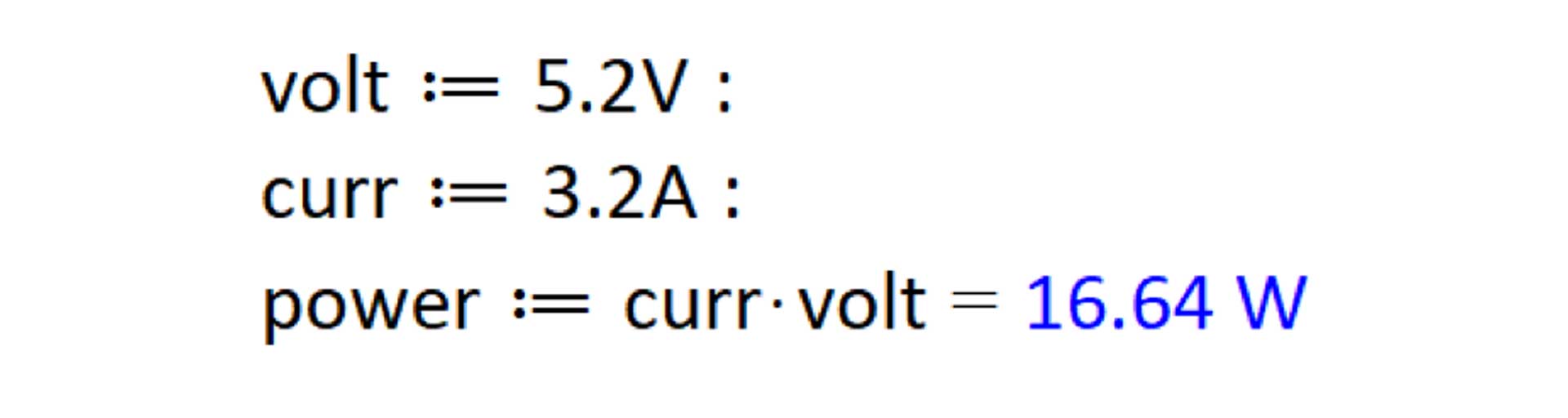
Figure 3. Calculations with Units
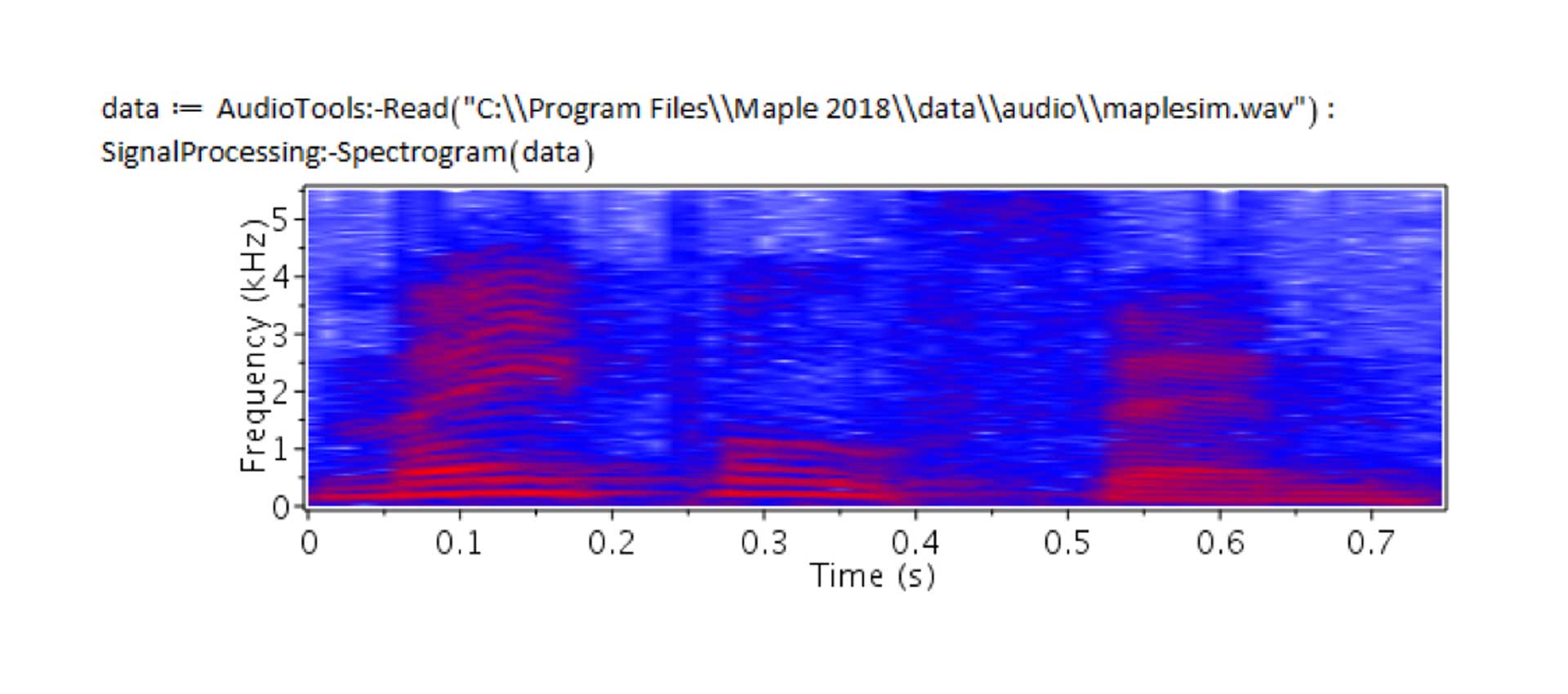
Figure 4. Importing audio and generating a spectrograms
You can import and export data to and from spreadsheets, text files, audio data and many other file formats.
Maple can also call externally defined code (for example external solvers or proprietary data sources defined in a DLL) and connected to dedicated process simulation tools.
Some electrical engineers use Maple to automatically transform SPICE netlists into mathematical expressions - a task that would otherwise be done by hand; these expressions can then be analyzed, manipulated and visualised in Maple.

Figure 5. Translating a netlist for a one-pole filter into a transfer function
Maple boasts a broad range of built in plots. These include:
These visualizations are fully customizable, and new plot types can be programmatically generated.

Figure 6. Polar plot of the directivity of an antenna array
Applications can be password protected, while still remaining executable. This means live applications can be distributed while the intellectual property remains securely locked away.
Applications can be distributed royalty-free as interactive desktop tools using the Maple Player, or deployed over the web.
Moreover, Maple will translate user-developed programs to C, Python©, Java and several other languages.
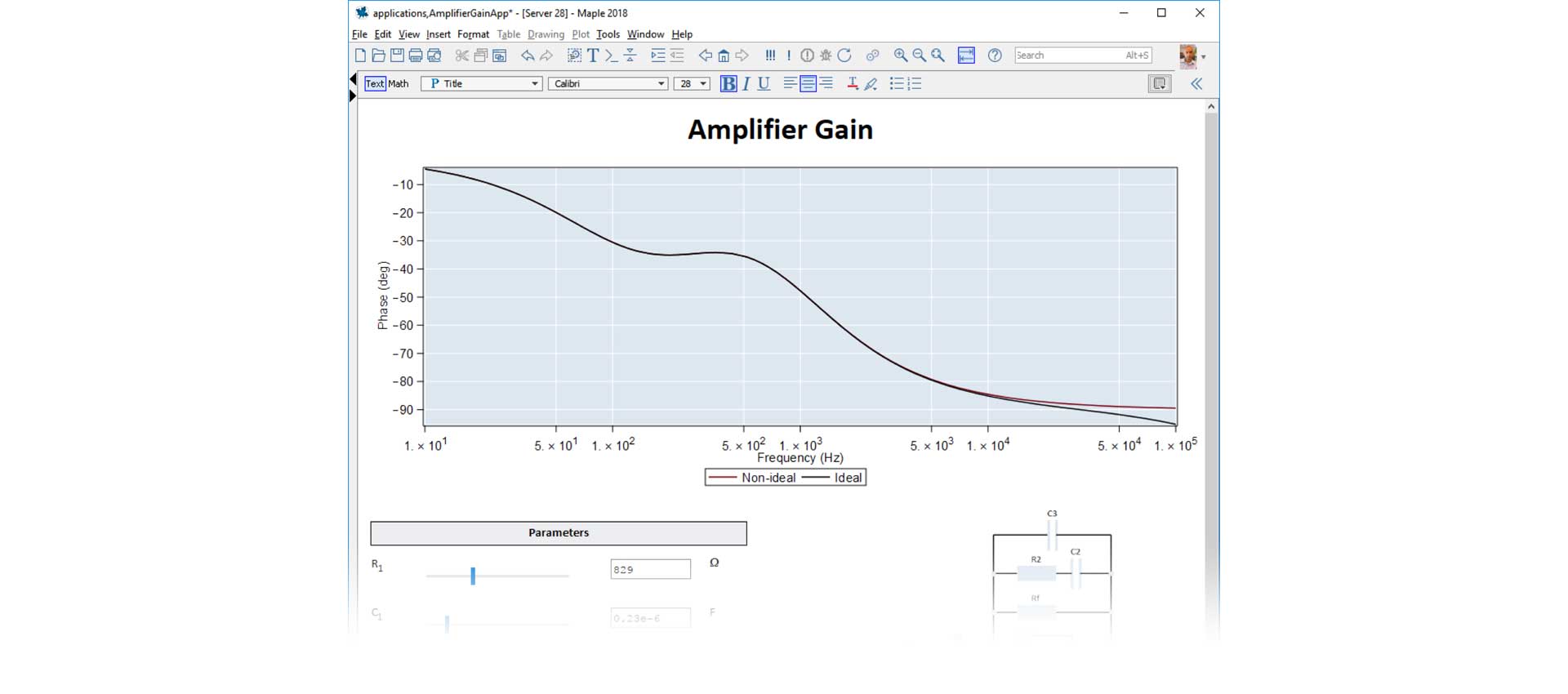
Figure 7. Deployable application for analyzing the gain of an amplifier
In this section, we will discuss how electrical engineers have typically used Maple. First, each application is briefly described. Then, the Maple features used in the application are discussed.
An electrical engineer wanted to calculate the optimum design parameters for an X-band pyramidal horn. The engineer entered the parameters and equations in Maple, and solved the resulting system numerically.
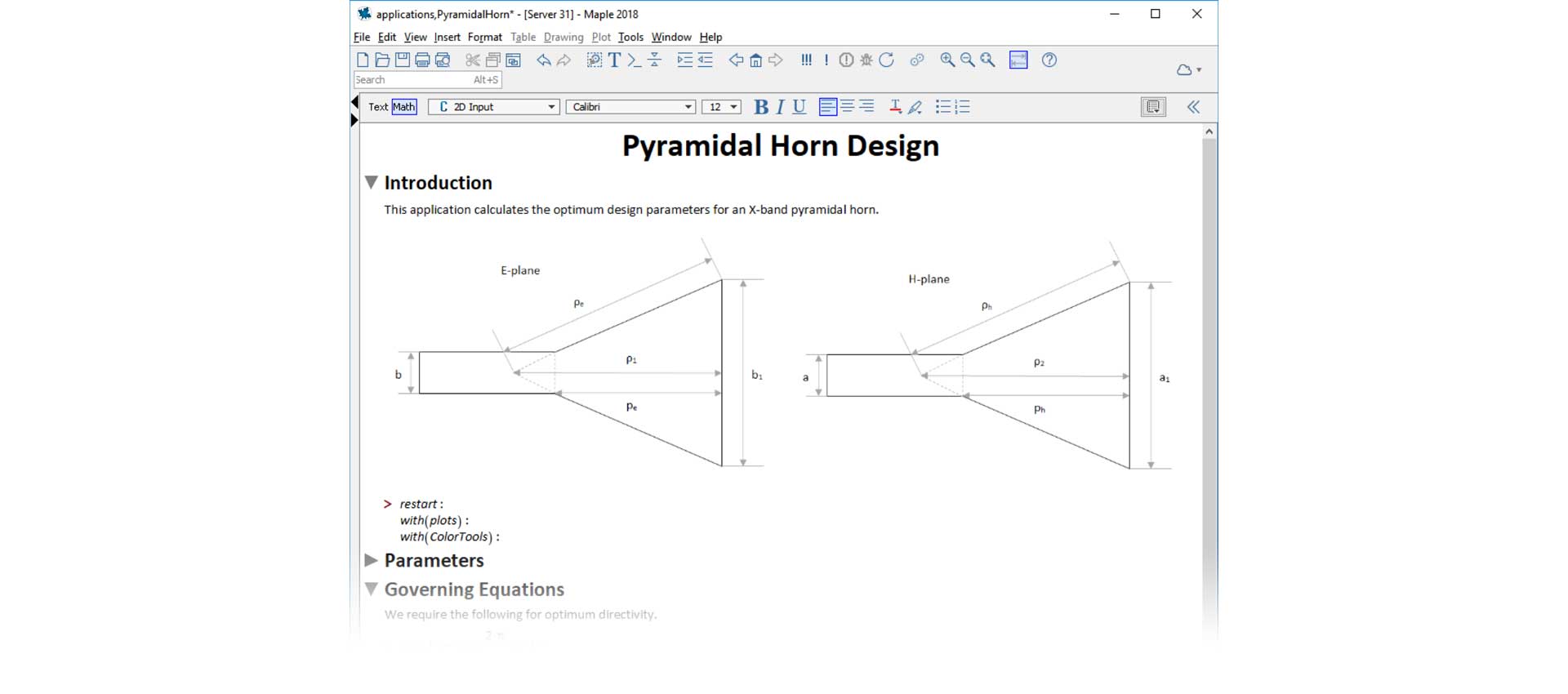
Figure 8. Design of a pyramidal horn
| Task | Maple Feature |
|---|---|
| Set up equations that describe geometrical constraints of pyramidal horn | 2-D math notation, units |
| Extracting speed of light | Built-in scientific data |
| Finding the optimum design parameters | Numerical equation solver |
| Visualize e-plane radiation pattern | Polar plot |
The governing equations involve parameters that vary by several orders of magnitude, and are challenging to solve. Maple's numerical solver, however, easily solved the equations.
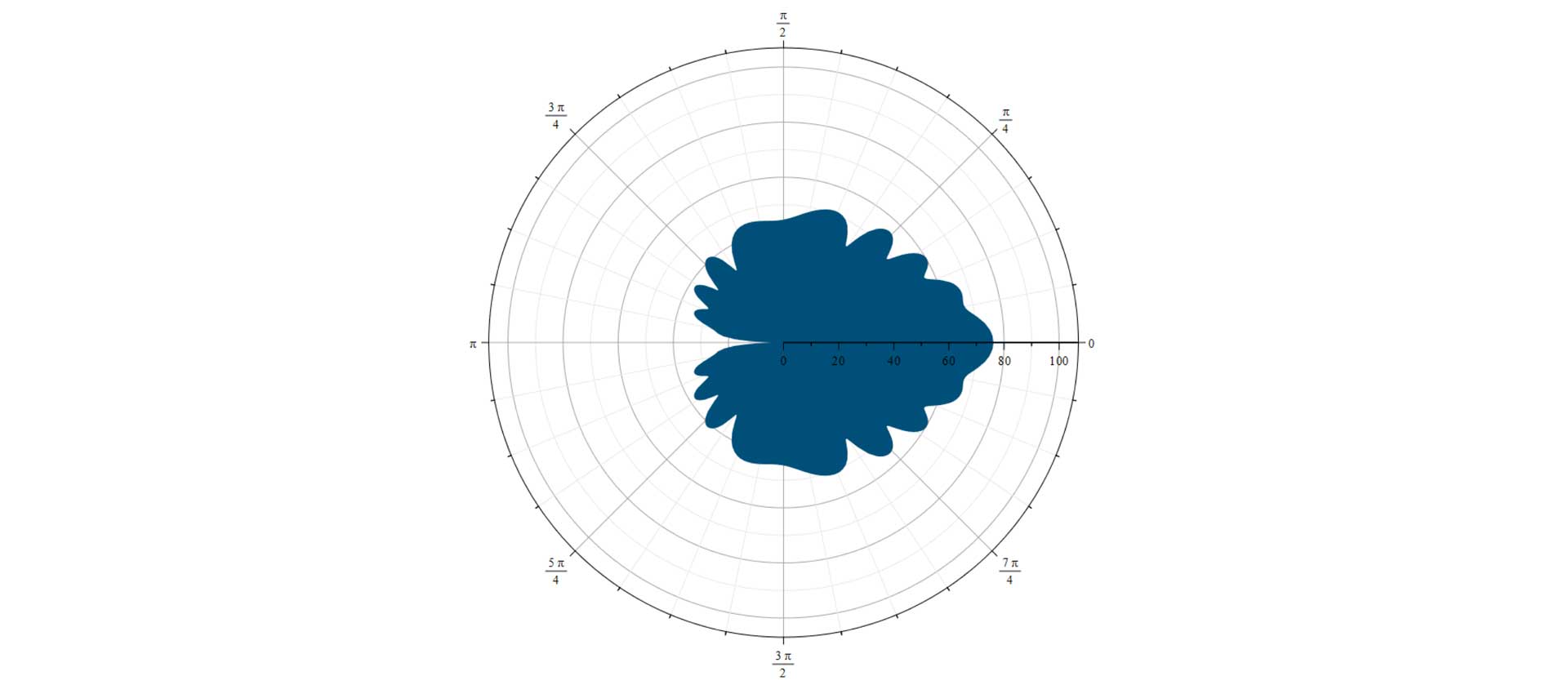
Figure 9. E-Plane radiation pattern for a pyramidal horn
An electrical engineer was tasked with developing a web-based app for coaxial transmission line. Specifically, the app needed to help the user determine the optimum dielectric material and the wire size.
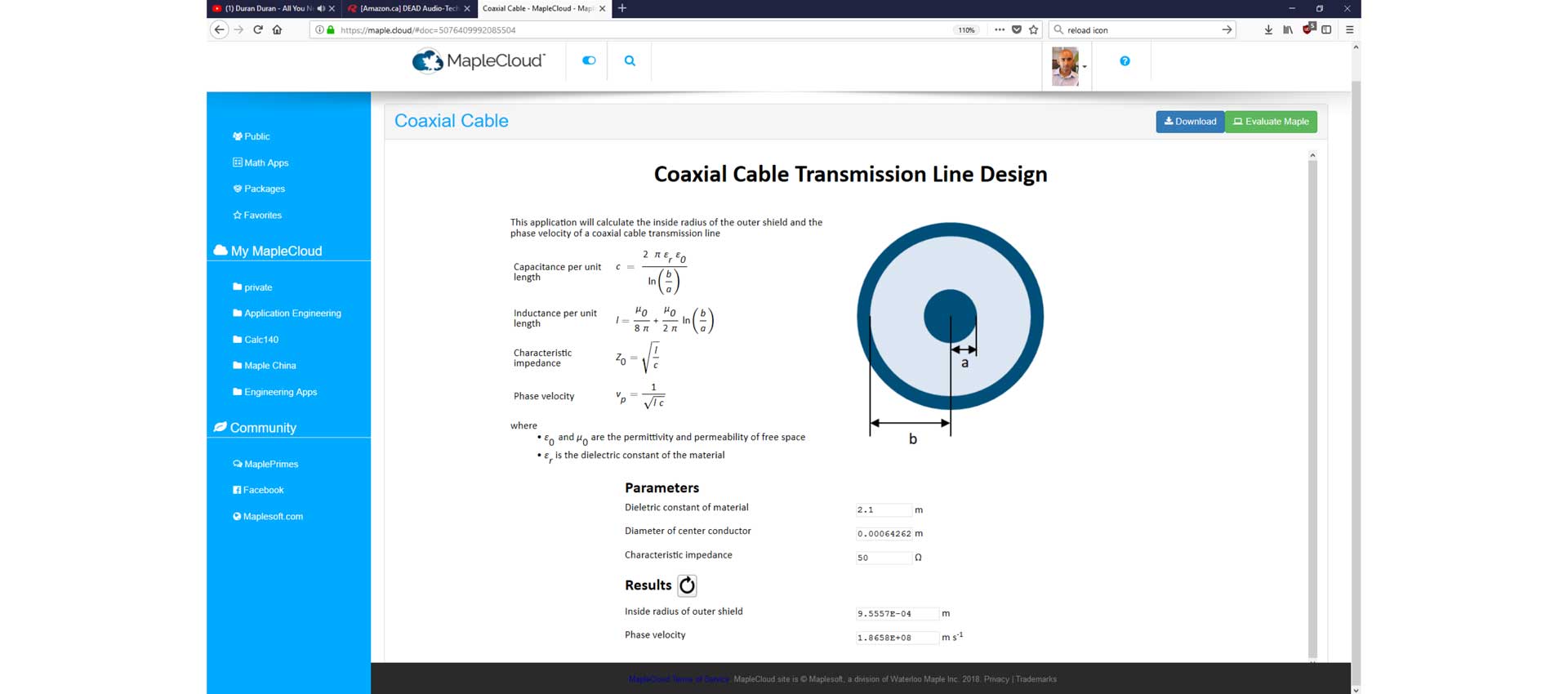
Figure 10. Web-Based coaxial cable transmission line design
| Task | Maple Feature |
|---|---|
| Develop a Maple application to find the dimension and phase velocity of coaxial cable | Programming language, user interface components, numeric equation solver |
| Values of permeability and permittivity of free space | Built-in scientific data |
| Deploy Maple application to web | MapleNet™ |
Given experimental values of the forward current (If) and voltage (Vf), an electrical engineer needed to estimate parameter values for a photovoltaic diode.The implicit photovoltaic diode equation needed to be rearranged before regression could take place. This used special functions only available in advanced tools like Maple.
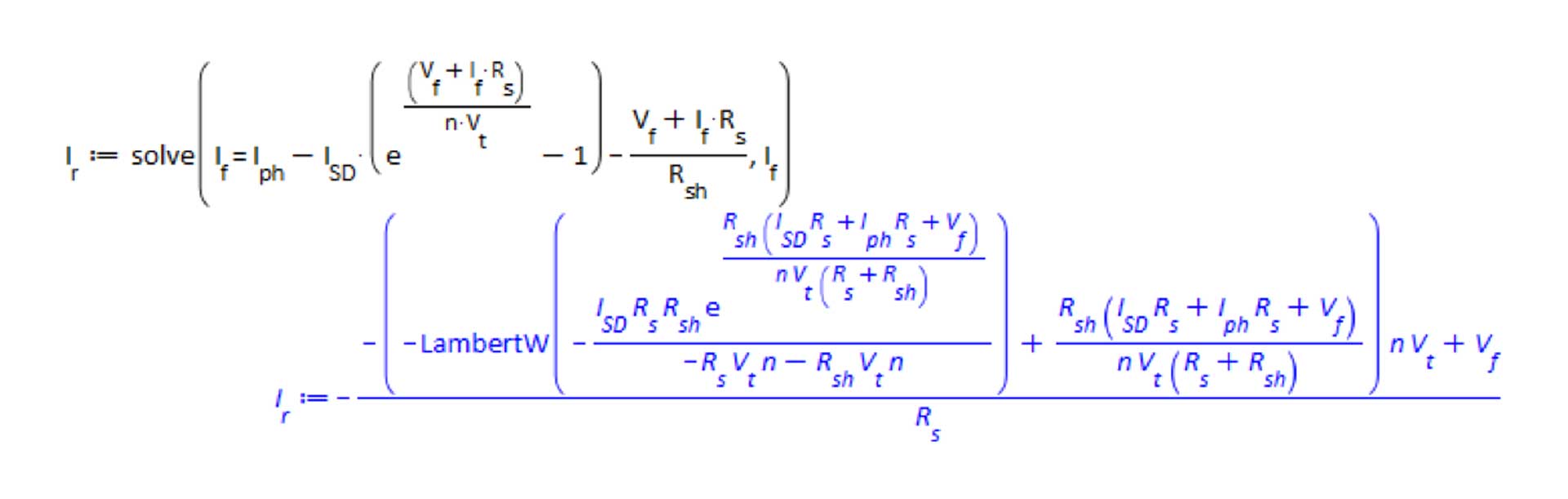
Figure 11. Rearrange photovoltaic diode equation
| Task | Maple Feature |
|---|---|
| Combine spreadsheet with experimental data and Maple worksheet into one file | Workbook file format |
| Rearrange the photovoltaic diode equation to give current in terms of voltage using the LambertW function | Natural math notation Symbolic math |
| Boltzmann constant and electron charge | Built-in scientific data |
| Regress experimental data to find best-fit parameters | Curve fitting and optimization |
| Plot experimental data and best-fit curve | Programmatic visualization |
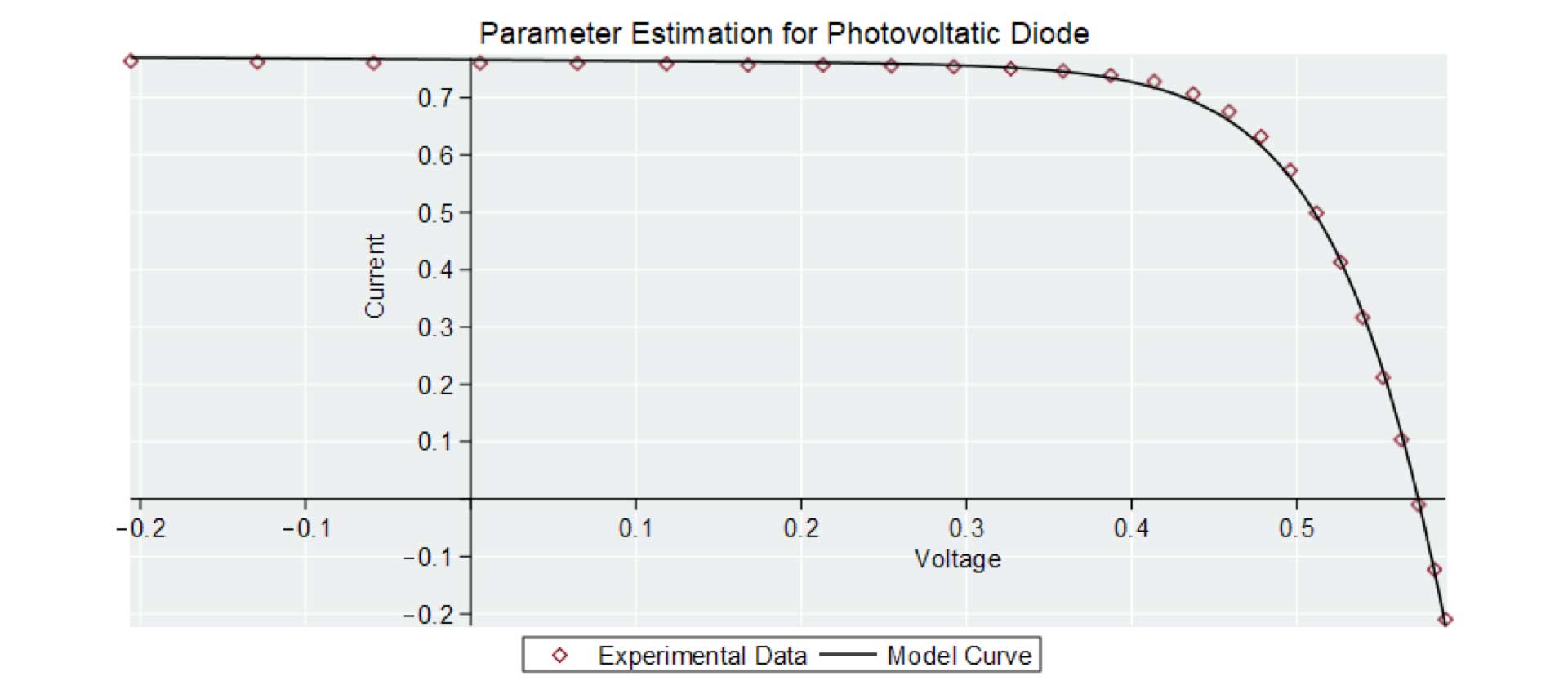
Figure 12. Parameter estimation for a photovoltaic diode
Calculations shape the engineered world around us. Calculations deserve respect, and accordingly need to be managed.
Maple provides a unique calculation environment that captures design intent, provides high-level math tools, and also offers cost-effective deployment targets
Fundamentally, Maple helps electrical engineers to manage their calculations. This transforms what would otherwise be an isolated analysis into a structured asset that can be reused, extended and shared with clients and colleagues.