
Learn More Maple’s technical documentation environment
Maple offers practical high-level tools for numeric and symbolic math, data analysis, and programming. These tools are designed for both simple and complex engineering problems.
The symbolic and numeric math engines are seamlessly connected; parameters, equations and calculations can fluidly flow between the two. This means you can derive and numerically evaluate your equations in a single cohesive workflow.
Moreover, Maple’s programming language benefits from an interactive development environment and can use any of Maple’s high-level math tools.
Nearly every single quantity an electrical engineer encounters – whether it’s a resistance, voltage or a length - has a unit. Units are fluidly integrated into Maple, and can be used in simple calculations as well as numeric equation solving, optimization and visualization.
volt := 5.2V :
curr := 3.2A :
power := curr volt= 16.64 W
Using units in calculations removes the risk of introducing unit conversion errors, and also acts as a check on the physical validity of the equations.
You can use Maple to derive and manipulate transfer functions of electric circuits using Kirchoff’s current and voltage laws. Transfer functions can be converted to differential equations or discretized, and you can easily generate Phase and Magnitude plots.
Transfer functions can contain symbolic coefficients; these parameters can be optimized to match a target response.
Maple contains many features to help you symbolically manipulate transfer functions. These include:
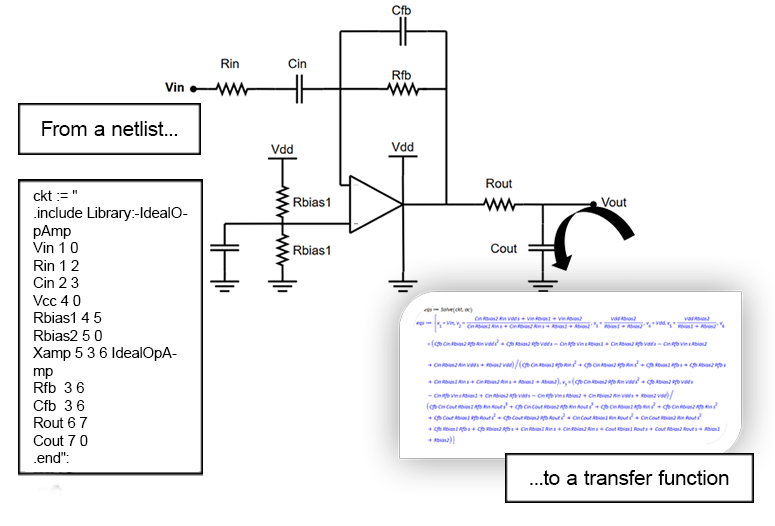
A free package for Maple lets you convert SPICE netlists to transfer functions. This transfer can be analyzed in Maple’s symbolic and numeric math environment. For example, you can do AC and DC analysis, generate phase and magnitude plots, rearrange the transfer function for specific parameters or convert it to a differential equation and more.

Semiconductors are complex devices, but Maple helps you derive the math models to accurately describe their characteristics.
MOSFETs are a critical component of modern electronics such as smartphones and other portable devices. Low power MOSFETS are critical to switching in power supply systems.
With Maple, you can turn equivalent circuit models of MOSFETS into analytical equations by writing down and manipulating the basic relationships.
These applications, for example, will help you model the effect of source inductance and cross conduction in modern power MOSFETs.
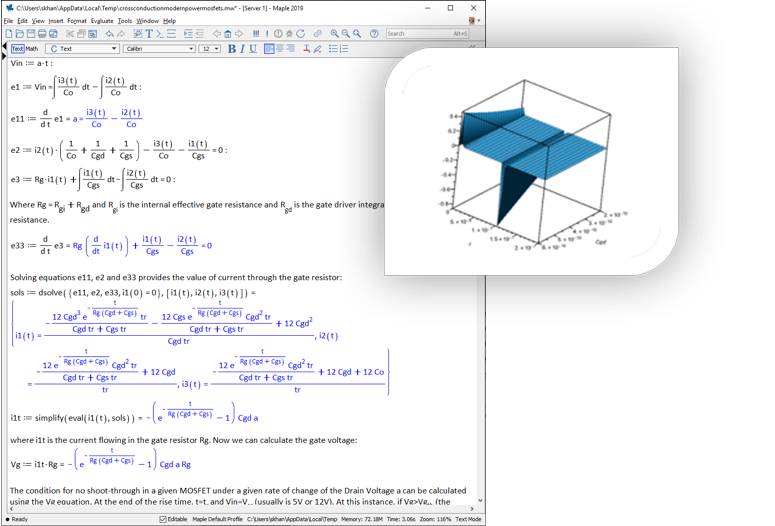
Deriving the equations for the gate voltage of a MOSFET
Electrical components are manufactured in large quantities. Inconsistencies in the materials and the manufacturing process mean that component parameters have a statistical distribution. That is, the resistance of a batch of resistors might be described by a normal distribution.
Given the number of components in a circuit and the distribution of their parameters, the circuit may not perform as specified. This is a risk that must be identified, managed and mitigated early in the design process.
Electrical engineers often use Maple for worst case circuit analysis. You can either employ:
Once prepared, you can automatically generate a table of results and populate it with the results of your analysis, including conditional coloring for out-of-specification parameters.

Practitioners in antenna and radar design use Maple to create executable design documents that capture the spatial, temporal and spectral aspects of their designs. The documents can contain both the equations, programming and visualizations necessary for the design.
The design documents can be deployed to the web or the desktop.
