
Nearly every quantity an engineer deals with has a unit. In fact, dimensionality is a fundamental characteristic of engineering calculations.
However, most calculation software tools do not understand the concept of dimensionality; unit conversions and consistency checks need to be done manually.
In this whitepaper, we will demonstrate how Maple is a units-aware calculation tool that solves problems with units that engineers encounter in other software.
This is especially onerous with spreadsheets, where:
In the worst cases, unit conversion errors can lead to engineering disasters. For example, in 1999, NASA lost a $125 million space probe because one team worked in metric while another worked in US Customary units. While your unit conversion errors may not be as disastrous as those suffered by NASA, they're still frustrating, time consuming and a source of risk. And every engineer has an ethical duty to reduce risk.

Simply by using units-aware calculation software throughout a technical analysis, you eliminate unit conversion errors and provide a check on the physical validity of your equations. This saves time, removes a source of frustration and increases the reliability of your analyses.
Before you start a project, make sure your calculation tool understands units. Here's what to look for.
Equations should be presented naturally, and in a form that requires little cognitive overhead to understand.

You should be able to add or subtract parameters with the same fundamental dimensions, with all unit conversion done automatically.
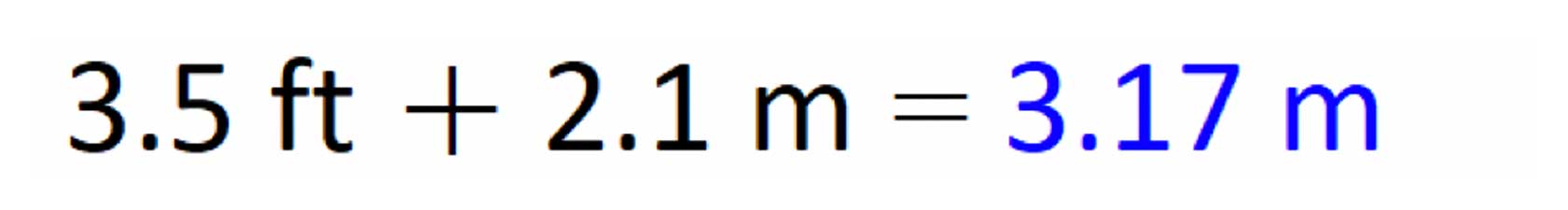
Results should be easily converted into different units, preferably with as few mouse clicks or keystrokes as necessary.
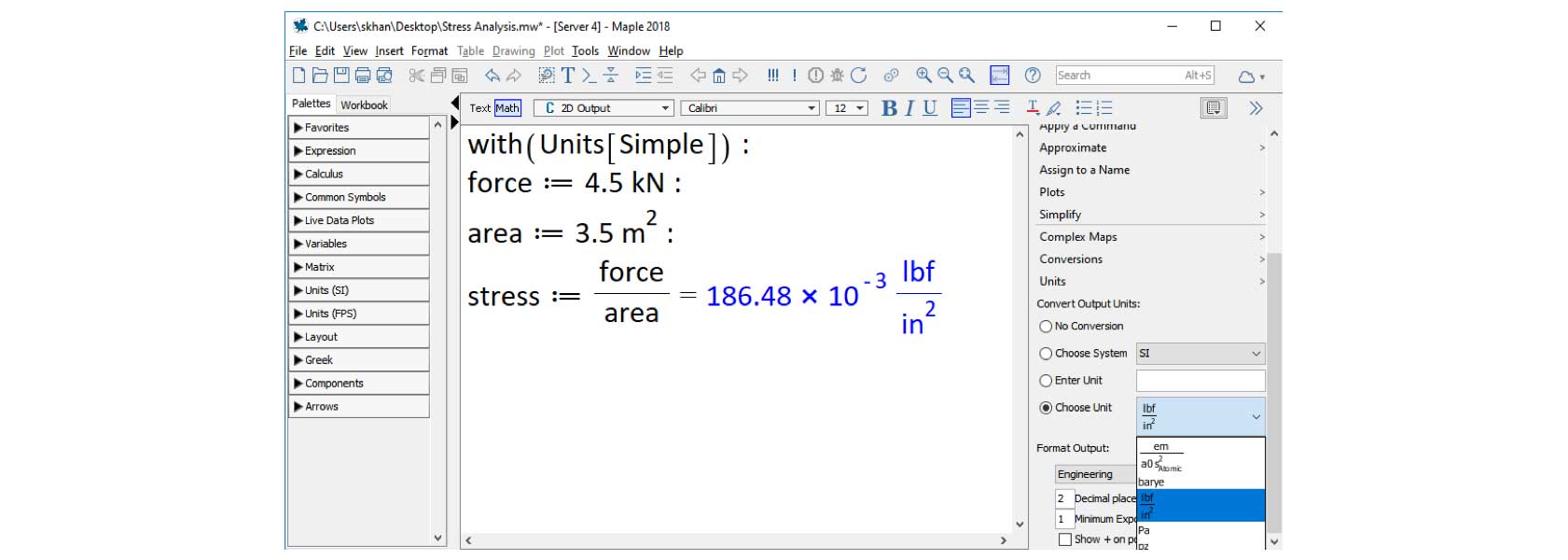
Compound units should, when appropriate, be automatically reconciled into simpler units. For example:

Your calculation software should tell you if you're trying to add quantities that don't have the same units, and refuse to proceed until you've corrected the error.

This is a simple check to ensure your equations are physically valid.
At the very minimum, your calculation tool should understand the entire range of SI and US Customary units (with, of course, a smooth flow of calculations between both unit systems).
Some niches in chemistry and physics use the CGS or Atomic unit system; these should preferably be supported as well.

Engineering systems often result in sets of equations that demand numerical solvers, integrators or optimizers. For example,
Accordingly, these computational routines should understand units.
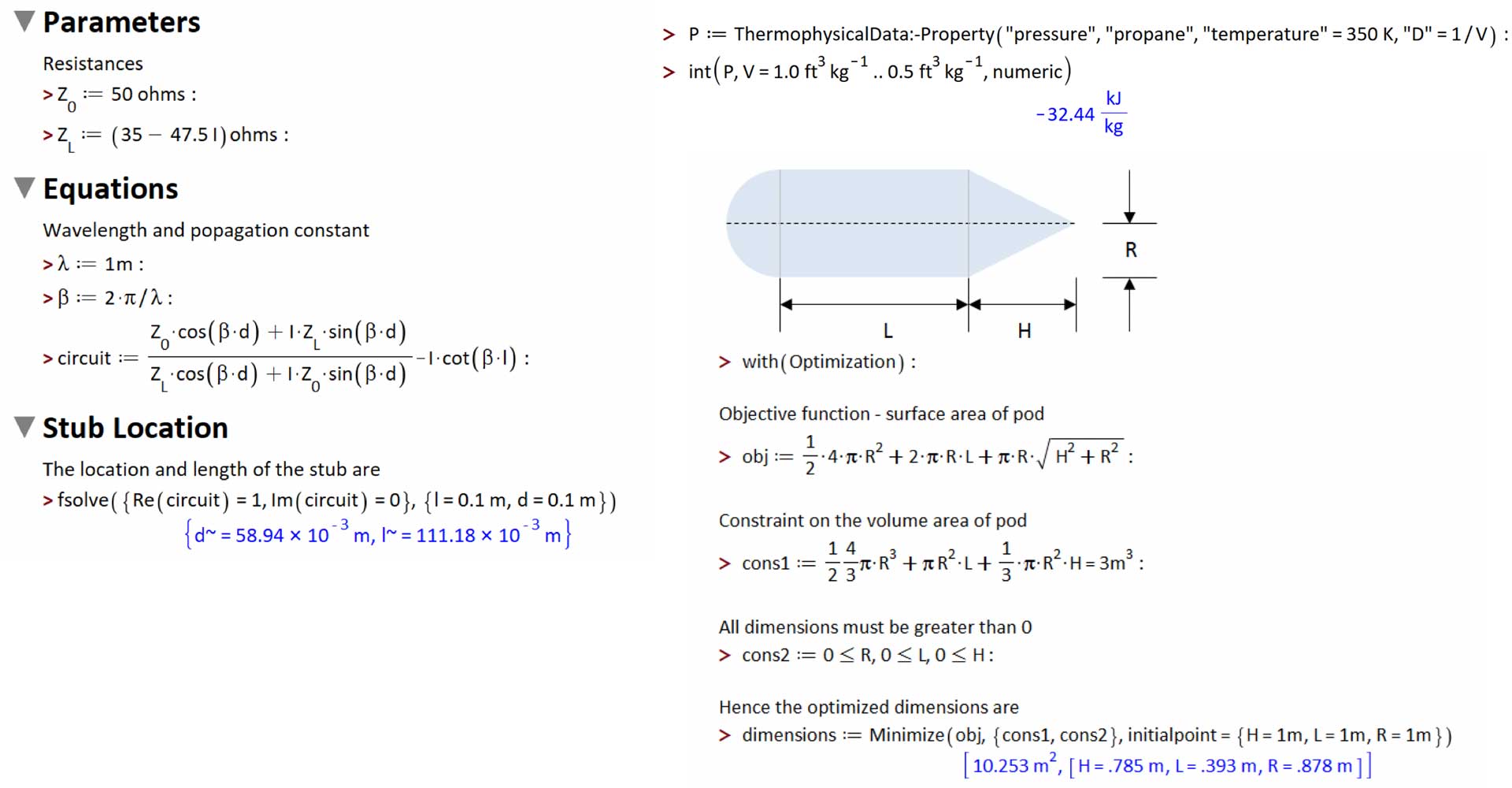
Engineers and scientists often employ libraries of data in calculations. Some examples include:
Any collections of scientific or engineering data built into your tool should include, wherever appropriate, unit information.

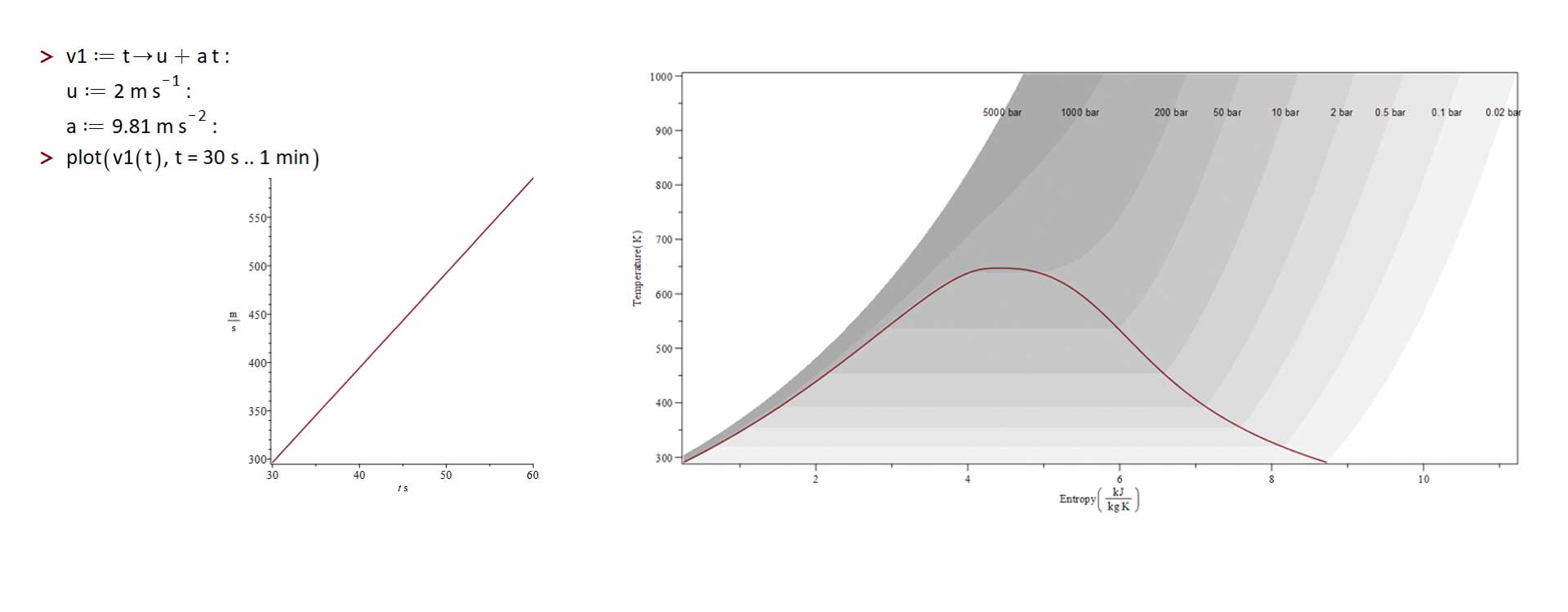
Units should be supported in plots and visualization routines, with dimensions clearly indicated on axes labels.
Calculation software tools already provide high-level tools for math, programming and visualization. Very few of these tools, however, understand units.
A lack of units in your calculation tool can introduce a source of risk into your technical analyses; the probability of unit-conversion errors increases rapidly when analyses are shared within and between teams.
Maple is a units-aware calculation tool, and was used to produce all the examples in this article. With Maple, units can be associated with parameters, carried through an analysis, and used in numerical solving and optimization. By using Maple, engineers eliminate unit conversion errors, saving time and increasing the reliability of their analyses.