"I Could Have Used This When I Was In School": Stories From The Maple-Deprived
Over my long career at Maplesoft, I have shown Maple to a lot of new employees. And whether they have a PhD in math or dropped math in high school as soon as they could get away with it, there is almost always a moment where the person stops, stares, and says some variation of “I could have used that when I was in school.”
So I decided to collect some of these stories as a way to show off the many different ways the math software Maple can benefit students. Like the students in your own classes, the people I talked to had a variety of backgrounds, mathematical abilities, and interest in math. These stories come from R&D, sales and marketing, and customer service. They come from people who use Maple every day and those who have never even installed it. They come from people with advanced math degrees, and from people who hated math in school and are astonished to find themselves working for a math software company now.
Note: I promised I wouldn’t use names because some people really hate that, but these are all stories from current or former Maplesoft employees. I helped write some of their stories, based on our conversations, but everyone has approved their quote.
The first story is mine.
I’ve always liked abstract math – the more abstract, the better (category theory was very satisfying). It never bothered me in the slightest that there was no physical interpretation to most of what I learned. In fact, I preferred it that way. I’m simply not a very visual person, in defiance of the math-ability stereotypes, and trying to visualize things can sometimes feel like I’m fighting my brain’s natural thought patterns. I can do it, but it’s a lot of work.
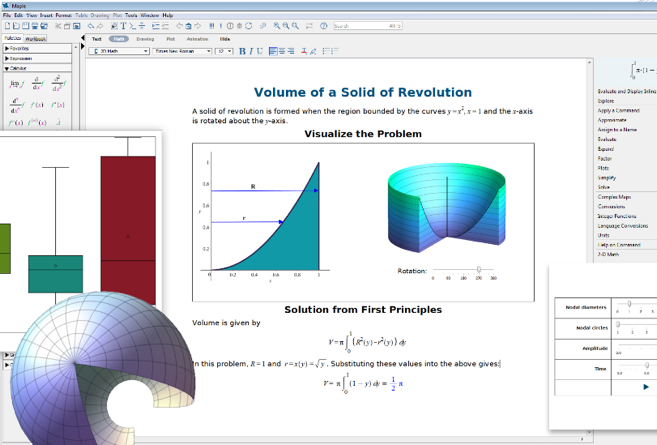
So I experienced a powerful “I could have used that!” moment the first time I saw a version of this interactive “slider plot”.

I had a flashback to sitting at my desk, calculating sample data points on my calculator and sketching tiny little graphs in the margin of my notebook, so I could figure out if the parameters in my trig function changed the amplitude, the period, or the phase shift, and how. I had no problems with the general concept, but I had a harder time remembering which parameter did what. Unfortunately, it took so long to create the sample graphs that I couldn’t do enough examples to get to the point where I didn’t have to think about it anymore. I’m convinced that a few minutes of playing with that slider plot would have really helped.

Of course, unlike me, some people need the visuals:
The Math App they were referring to was examining the root of quadratic equations:
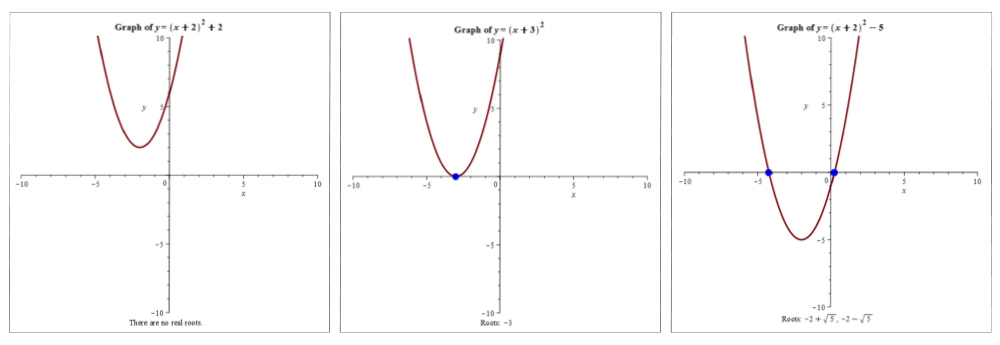
This App shows how a quadratic can have zero, one, or two roots, depending on how many places the curve crosses the x axis. When they saw the curve move from above the axis, to just touching, to below the axis where it crossed in two places, something finally clicked.
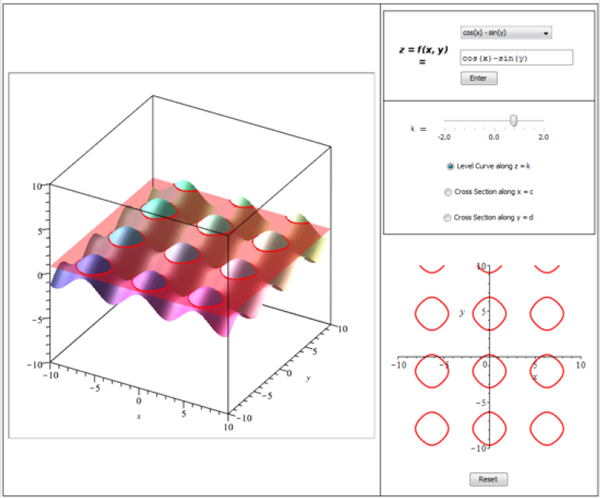
There is no doubt that visualization helps with understanding many mathematical concepts. But sometimes the understanding the student is looking for is not some new math concept, but simply “Where did I go wrong?”
For the most confident students, the first question isn’t necessarily “where did I go wrong”, but “did I actually go wrong?”
Sometimes understanding comes from the “aha” moment, but most often it comes through practice, and lots of it. But opportunities for meaningful practice can be hard to come by.
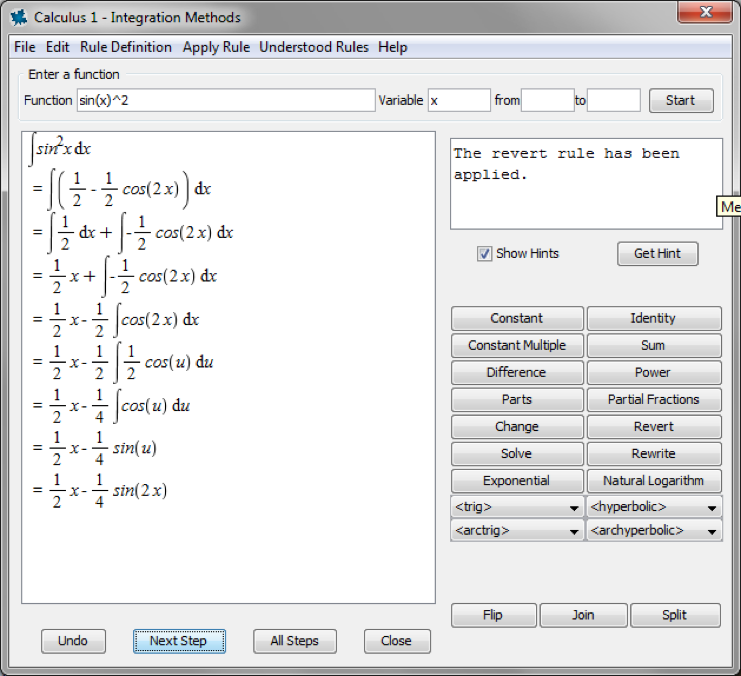
Integration practice, in particular, came up more than once in the conversations I had:
Students are busy, so it’s no surprise that many of the stories people told me revolved around ways that Maple could have saved them time and helped them work more efficiently.
Sometimes the issue is that students are forced to use an unnatural approach to solve a mathematical problem.
Similarly, it is frustrating to be forced to perform a repetitive task manually when a better method is available:
Maple can certainly help students solve problems faster than by hand, but Maple can also help save time over the entire assignment.
And it’s not just the students’ handwriting that can be problematic.
Underlying these anecdotes is the feeling that, while a student may be perfectly willing to pour hours of work into a course, they want to feel like that time isn’t wasted. Performing a task in a slow, inefficient, or unnatural way takes up time that could be better spent on activities that have a greater impact on their learning, such as reviewing the day’s lecture notes, trying additional practice problem, checking over their assignment, or even getting a reasonable amount of sleep.
While it wasn’t necessarily what these contributors were thinking at the time, many of these stories can be viewed as “Maple would have given me more confidence”: Confidence that my answer is correct. Confidence that, if my answer is not correct, I will be able to fix it. Confidence that I’m not wasting my time. Confidence that comes through practice. Confidence that I really understand.
Maple helps students understand new concepts, build up their skills through practice, check their answers so they know if they are right, and if they are not, Maple gives them tools they can use to discover where they’ve gone wrong. All these uses of Maple contribute directly to students succeeding in their courses. But it’s important to note that these activities also help develop a student’s confidence in their mathematical abilities. Since it’s well established that confidence, or lack thereof, makes an especially big difference to student success in math courses, the fact that Maple can help develop a student’s confidence is far more important than any particular feature or example.
I’ll end with another story from my own experience.
My high school, unlike any other school I’ve ever come across, told students who were struggling with math to take Calculus if they needed a single math credit in their final year to get into their chosen post-secondary program. When I took high school Calculus, about a quarter of the class was taking the course for the second time, and still struggling. The students like me, who were good at math, coasted through the course without ever having to think too deeply about what we were doing (actually, we played a lot of Euchre during the abundant work periods). Combined with my natural tendency not to visualize anything if I wasn’t forced to, this experience left me ill-prepared for my extra-advanced Calculus course in first-year university, where the professor started every class by putting a poorly behaved function on the blackboard, and asking us to figure out what it looked like. He kept saying things like “can you see that, as x gets close to zero, this term will dominate?”, “can you see that the curve will bend like this at about this point?”, “can you see that…?”. At that time, I still had to think for a moment to be sure I wasn’t getting logarithms and exponentials mixed up, so my answer to “can you see that…?” was invariably “no”.
So then I had two problems. First, I was genuinely less prepared for this course than many of my classmates, and second, my confidence in my ability to succeed in that advanced class was quickly destroyed, which in turn started to seriously affect my performance in the course as a whole. I got through it, eventually, but it was a real struggle for most of that term.
If I had had Maple*, I could have used a systematic approach to build up my plotting intuition – something I hadn’t ever realized I needed and was missing. I could have tried plotting example after example of basic functions, immediately seeing the effect of varying parameters, and combining expressions like we did in class. I could have guessed what they would look like and then checked how my answer compared, until I no longer had to think so hard about every little thing. That understanding would have definitely helped. But what I think would have made an even bigger difference is that I would have felt a whole lot more confident in my own abilities relative to my classmates, and hearing “can you see that…?” would have stopped filling me with such a sense of dread even if the answer was still “no”. (Which it probably would have been often enough - he picked some truly pathological functions!)
The people in this article did not have access to today’s Maple throughout their education, but they all felt that having Maple would have made their student experience better. Your students are fortunate, because they can have these benefits today, instead of looking back years later and saying “I could have used that”. However, if your students don’t already have access to Maple, they likely need your help, or at least your encouragement, to get this better experience. It’s something to think about.
* To be fair, technically I did have access to Maple around that time, though I didn’t realize it. But ASCII-rendered plots scrolling past the top of green CRT terminal would not have had the same illuminating effect.
Eithne Murray has been around Maple for much of her academic and professional life, such as using Maple for her Master’s thesis in computational number theory, helping develop Maple’s combinatorial structures package, and contributing to a textbook on using Maple in discrete mathematics. She has worked for symbolic computation research labs in France and Canada, and has held a variety of roles at Maplesoft in both R&D and marketing. She still isn’t particularly fond of visualization, but since the widespread availability of GPS technology, she gets lost much less often.


Learning math is not just about getting the answer, so in addition to its computation abilities, Maple also provides specialized student packages that offer focused learning environments in which students can explore and reinforce fundamental concepts in the same way their instructor does in class. Student packages are available for calculus, precalculus, linear algebra, statistics, vector calculus, multivariate calculus, numerical analysis, and more.
Many of these student packages include interactive tutors for exploring, understanding, visualizing, and practicing concepts. The Integration Methods Tutor is an example of a tutor that provides guided step-by-step problem solving. Maple also provides step-by-step tutors for differentiation, limits, inverting matrices, Gaussian elimination, linear system solving, and others.
Maple is a symbolic computation system, which means it is capable of manipulating symbols, such as x and y, not just numbers. As a result, problem solving in Maple is a lot more natural than numeric computation systems like MATLAB, because the student can express a problem the same way they would on paper, and the results are expressed as proper mathematical expressions, not just numbers.
Maple includes over 5,000 computational functions covering virtually every area of mathematics, as well as many specialized applications, including:
…and many more. Maple also includes a programming language that was designed for mathematics, which can be used to customize and extend Maple’s abilities.