
How Technology Helps You Help Your Students
Math matters, both to our world generally, and to the individual future success of your students. That’s why, as educators, you strive endlessly to help your students understand and work with math. It’s important and rewarding work, but it’s also a challenging task that becomes especially difficult when class sizes grow, distractions multiply, and the effects of learning loss continue to be felt. Fortunately, the right technology can act as your assistant, providing a greater return on the investment of time and energy you put into teaching, and helping you help your students succeed.
In this whitepaper, we will examine seven extremely common challenges faced by instructors who teach math and courses that make use of math, such as engineering, physics, chemistry, business, and economics. For each challenge, we will show examples of how the Maplesoft Mathematics Suite, a collection of software solutions from Maplesoft, can provide enlightening visualizations, instant feedback, motivating examples, hands-on explorations, and other supports that can help you conquer that challenge. To illustrate these examples, we provide screenshots and short video clips taken using a variety of products from the Suite. If you want to learn even more about these and similar examples, watch the recorded webinar Math Matters, So How Can you Help Your Students Succeed?
When it comes to math education, whether you are teaching a math course or a course that relies on mathematics, seven very common challenges experienced by educators are:
You can’t manage these issues by investing more time into your classes. Where would those hours come from? But math technology can help in each of these areas.
Students have a lot of demands on their attention, even during class. So much of what is on their phones and laptops is designed specifically to lure them away when you need them to pay attention, and for a lot of students, “a bunch of equations” is not exactly gripping.
But math can come alive. It can be visual. It can be interactive. It can be fun to mess around with, just to see what happens. It can sometimes even inspire students with its possibilities. But for that, you need more than a static page. You need something dynamic, with enlightening visualizations and meaningful interactivity.
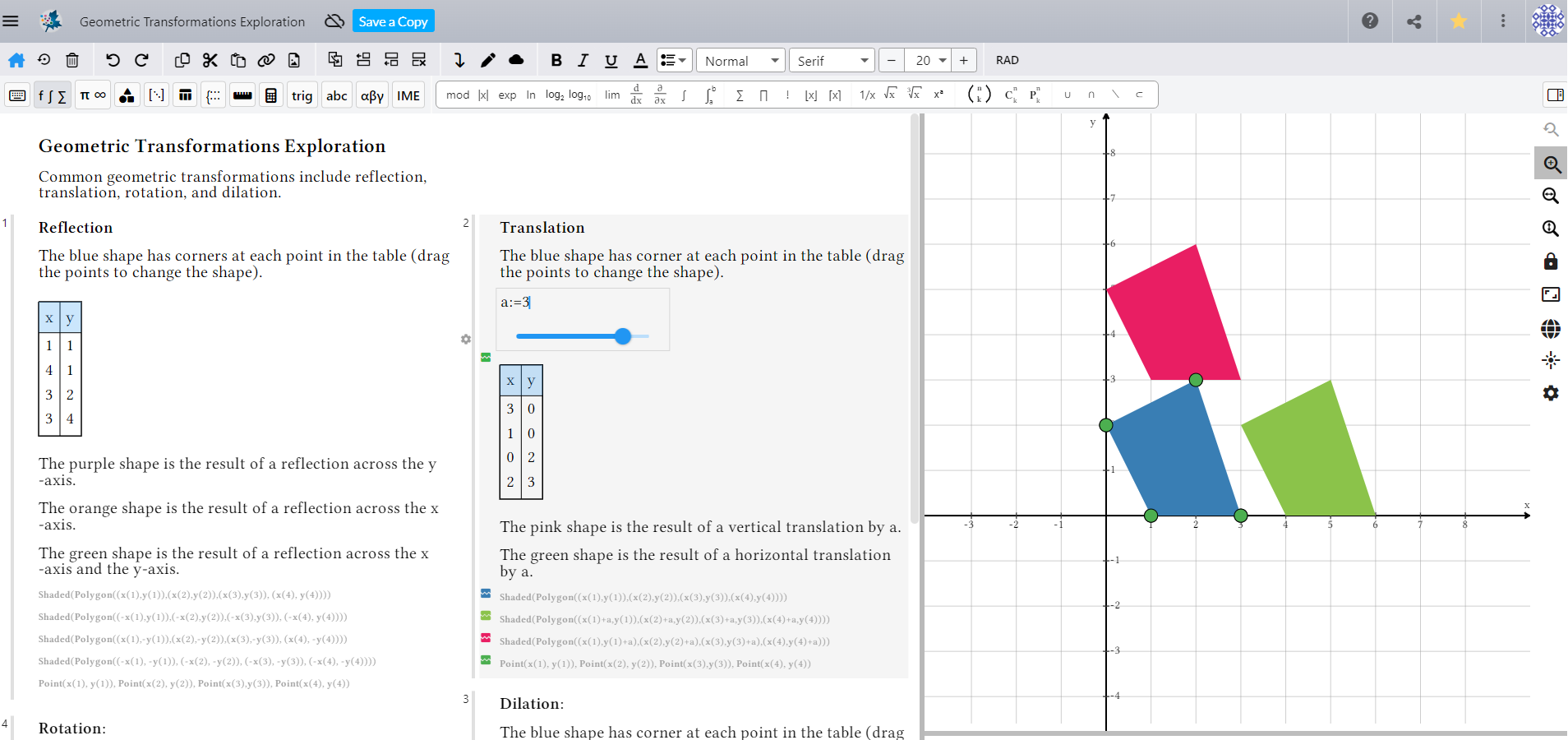
In this example demonstrating geometric transformations, students can perform reflections, rotations, and dilations for themselves, and see the results instantly. For instance, they can create a shape and see it reflected across the x-axis and y-axis, translate a shape horizontally and vertically by moving a slider, or move a different slider to set a dilation factor and see the results.
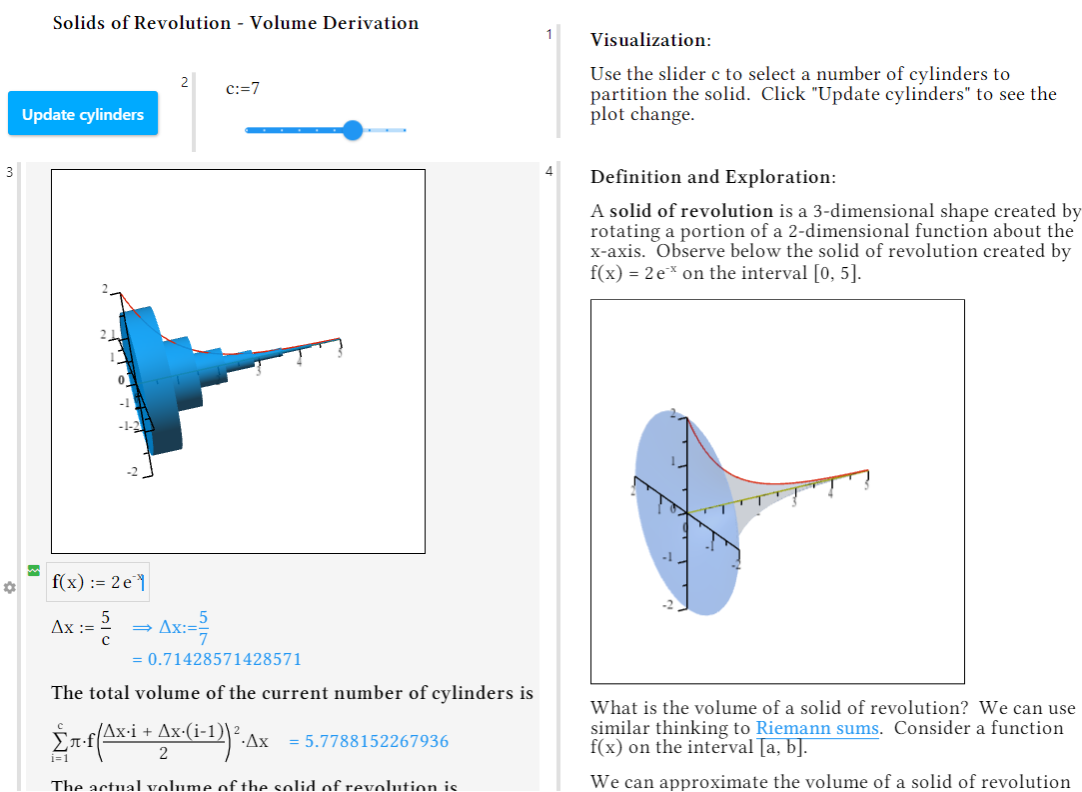
Students often struggle to visualize solids of revolution, and instructors have twisted themselves into pretzels trying to convey the concept. In this example, students can watch how the 2-D curve is rotated to form the 3-D shape, and then rotate the resulting image themselves to get a good look from different angles. They can see how the cylinders approximate the shape, and increase the number of cylinders to see visually, as well as numerically, how the approximation improves.
You’ve no doubt heard many variations of “But what is this stuff good for?” in your class. A few students may be quite happy to learn math for math’s sake, but most want to know why they need to learn what you are teaching them. What is it for? Why should anyone care?
Of course, math is used everywhere, and real-world applications go a long way to motivating students. Unfortunately, most realistic examples are far too complicated to work through in class by hand, and sometimes involve math the students haven’t learned yet. But with the right technology, you can present your students with motivating applications of the concepts you need them to learn, without anyone getting bogged down in calculations.
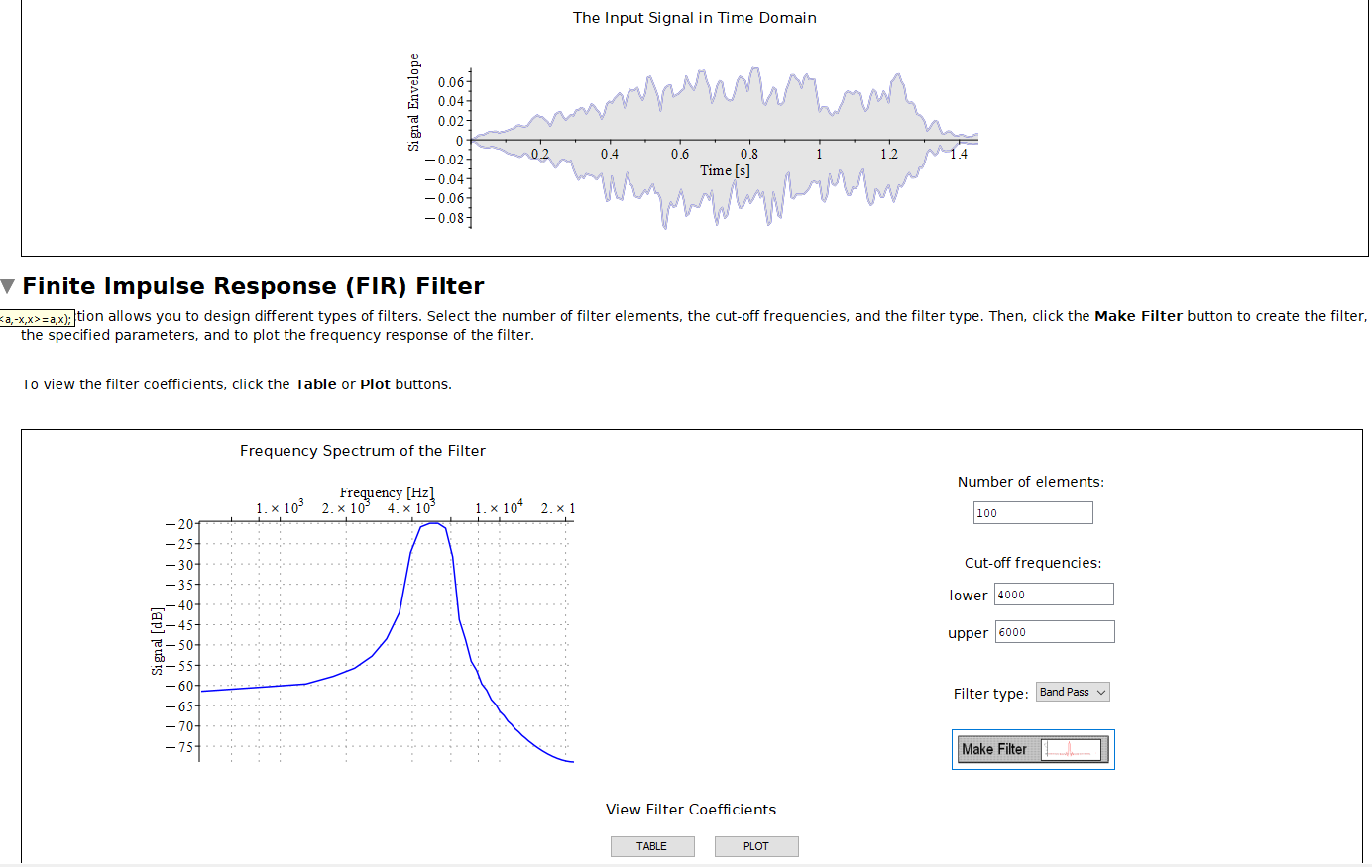
Fourier transforms and fast Fourier transforms can look like a lot of bothersome manipulations, and it can be difficult to convey their importance in a way that feels tangible to students. But almost all students have listened to muzzy sounding audio at some point. In this example, students design Finite Impulse Response (FIR) filters to remove the noise from an audio file that they can provide for themselves. They can experiment with the different filter types and settings without having to deal with the calculations yet, and see, and even hear, for themselves the results. In the end, students end up with a more intuitive understanding of what it means to remove noise from a signal, experience the need for different types of filters for signals with different characteristics, and have better conceptual understanding and more motivation to learn the math behind it.
Some students arrive in class anxious and stressed before you even open your mouth. Math anxiety is inhibiting their ability to learn, but there aren’t enough hours in the week to give these students a lot of extra attention. However, you can use technology to help improve their confidence by:
The student solves an integral on paper. They then ask a math tool for the solution, and if they are correct, they are reassured, and feel a little less anxious. If they discover that their answer is incorrect, the anxious student typically assumes that they just “don’t get it” and the anxiety and self-doubt is reinforced. But instead of stopping there, the student can take picture of their work using a math app on their phone, and upload the full solution to an online tool. There, they can ask the tool to check the full line-by-line solution, and the tool identifies where they made the mistake. In this way, the student sees both where they went wrong, and how much they did properly. If it was a small mistake, their confidence in their conceptual understanding is restored. If they do need to ask for help, they now have a more precise question, which makes it much easier for their instructor, friend, or other helper to assist them quickly, reducing the time the student spends feeling anxious.

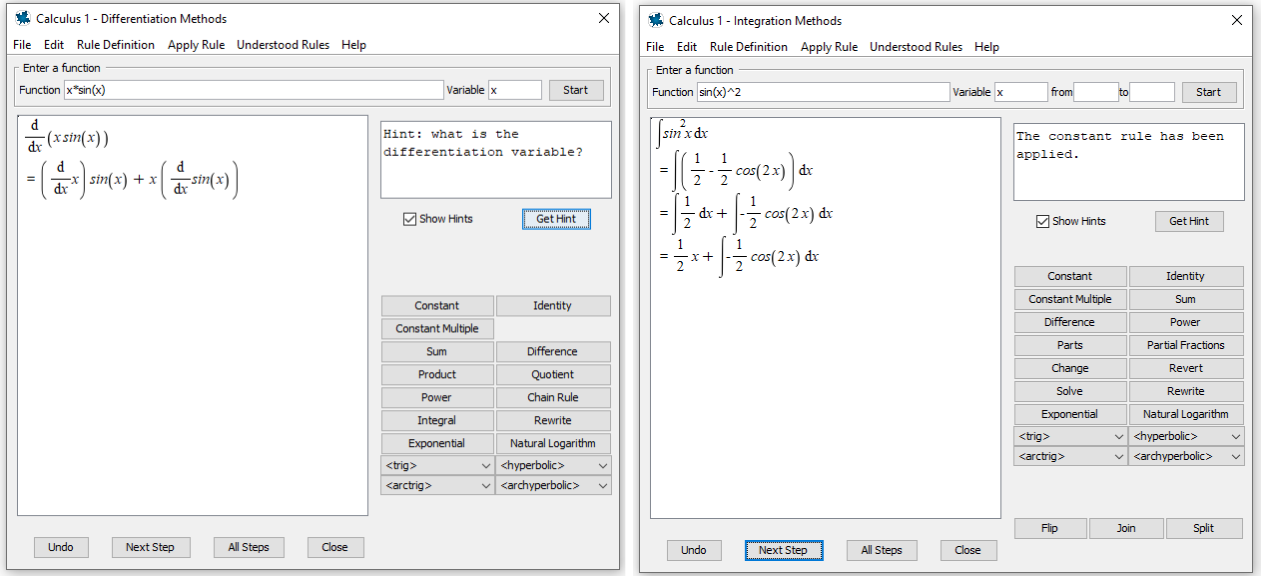
The anxious student tends to view every wrong answer as a sign that they don’t understand anything. Giving them a chance to practice the concepts separate from the calculations helps reinforce the important ideas without misplaced anxiety caused by simple mistakes. It also shows the student how much they actually do understand, so they can remain calmer later when a minus sign goes missing. In this example, these tools help student practice differentiation and integration rules, with a focus on understanding when to apply each method. The student picks which step to apply, and the actual calculations are performed by the tool so the student can stay focused on understanding how to work through problems at a higher level. If they are having trouble, the tutor provides a hint if the student makes a mistake, and the student can ask for a hint or for the next step, so they never get completely stuck and discouraged.
Some students can mimic what they learn in class, but have no real understanding of what they are doing, and why. They work through the steps, and reach an answer, but they are just going through the motions. If you change the type of problem slightly, either they won’t notice, or they won’t know what to do. You want your students to actually understand what they are doing, not blindly apply an algorithm.
In many cases, a good way to achieve the goal of understanding is to help the students visualize the concepts behind the steps, and technology can help you do that.
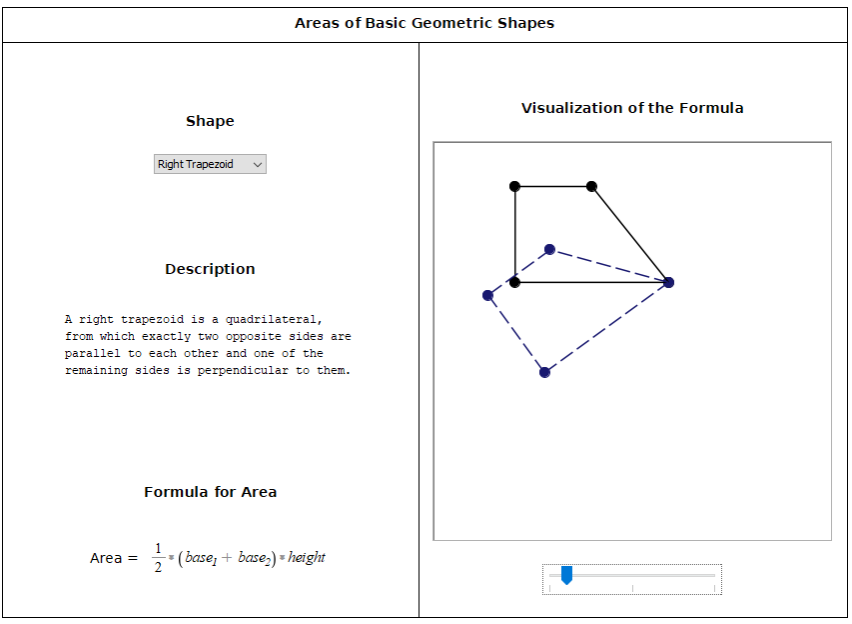
In this application, students can animate the geometric construction behind the formula for the area of a given shape. Now, instead of memorizing a bunch of seemly random formulas, they can see where those formulas come from, which will help them remember them, and also provide them with techniques for tackling more advanced problems.
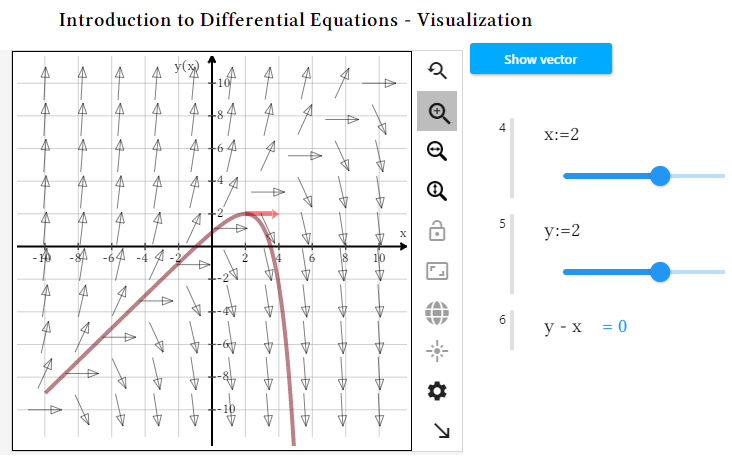
It’s one thing to follow the steps to solve a differential equation, but it’s quite another to “get” what is really going on, and why there are general solutions and particular solutions. In this example, students see a direction field for the chosen differential equation, the direction arrow at a specific point, and how the trace of an approximate solution through that point follows the arrows. They can experiment with picking different points and seeing how the vector and solution change each time. Developing their intuitive understanding through this kind of exploration provides students with a strong foundation on which to build further skills.
Visualizations that promote conceptual understanding are important, but you also need your students to roll up their sleeves and start solving problems. Lots of problems. But there are only so many problems with solutions in the textbook, and very often, that won’t be enough practice for some students.
With the right technology, students have access to an inexhaustible pool of practice problems that lets them practice as much as they need to. The tool will tell the students if they are correct or not, so they can build confidence as they build their skills. Even better, some tools can even help students understand where they went wrong and how to get back on track.
In this example, the tool generates a sequence of practice problems that are designed to give the students practice with a very specific set of skills: applying the product and quotient rules to find derivatives. The student first solves the problem on paper, then uses a math app on their phone to take a picture and upload it into the tool, and clicks on Check Work. The tool looks at each line of their solution, and in this case, tells the student that they made a mistake on the second last step. The student then sees that they applied the rules correctly but made an arithmetical mistake in their derivation. They correct the mistake in the document, check it again, and then move onto the next problem. The student can also ask for hints, and because the instructor choose to allow it, they can request to see the full solution when they need another example to help them understand.

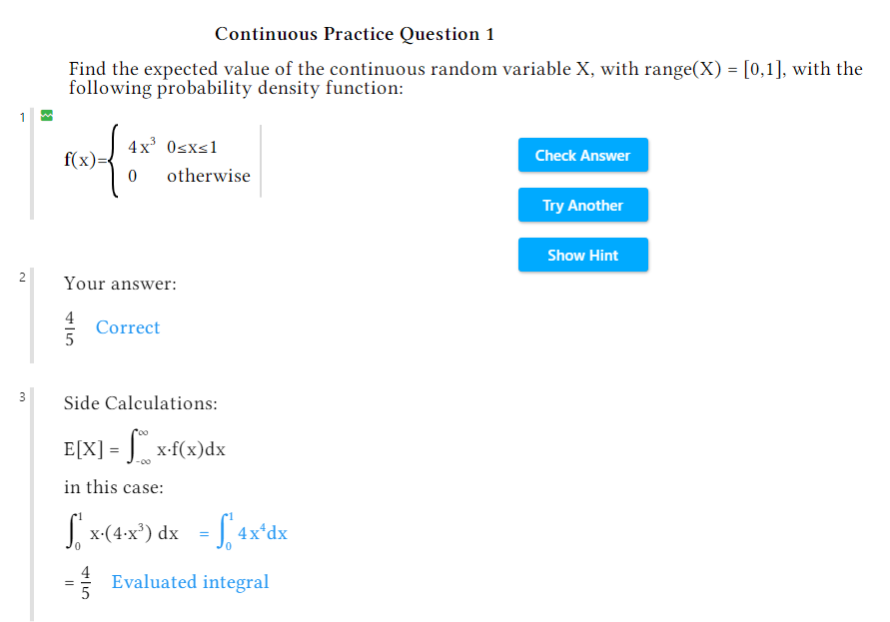
This document generates questions that allow students to practice finding the expected value of a continuous random variable, and then check their answers. Students first work out the solution inside the document itself, using a combination of manual steps and calculations performed by the tool. In this case, the instructor chose not to include the option to see full solutions, but did allow hints.
These days, your student can get answers to the standard “Solve this” type questions easily, whether they understand what they are doing or not. You can get a much better sense of your students’ learning by giving them tasks and projects that focus on solving conceptual problems. Often these projects will involve some combination of testing hypotheses, visualization, written explanations, calculations you want them to do themselves, and calculations you don’t want them to have to worry about. The right technology platform can provide you with the environment you need to set up interesting projects that your student cannot do simply by looking up answers. Instead, they need to think, and question, and communicate, and learn.
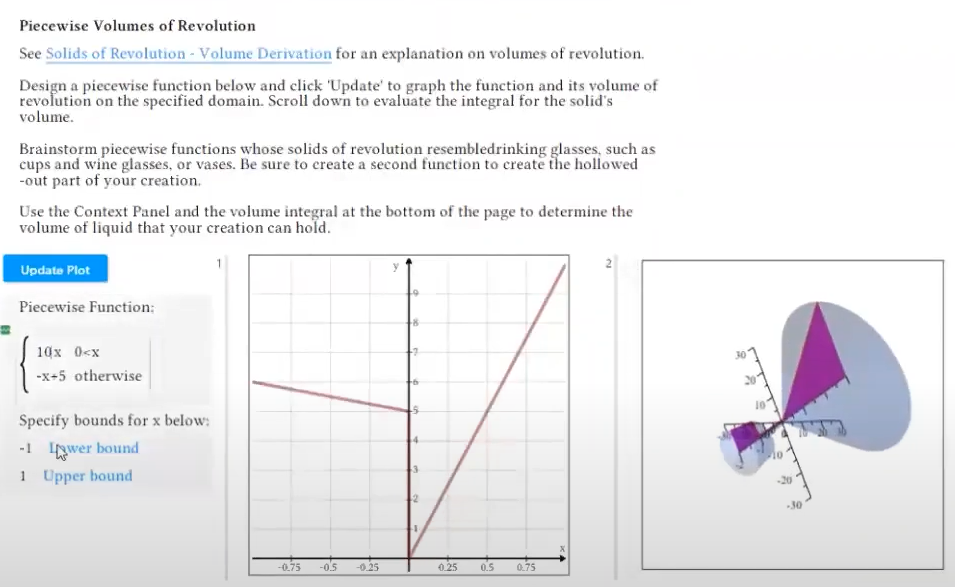
In this project, students are challenged to come up with a piecewise function whose solid of revolution looks like a wine glass or vase. Students can try out various functions, with various upper and lower bounds, and see the results. Very quickly they begin to think about how they would need to change the function in order to get a more desirable shape.
The instructor can also set a requirement for the minimum or maximum volume of the container, and students can use the software to set up and solve the integral to determine the volume of each shape, and then make further adjustments to their function to refine their glass or vase. Still in the same environment, the instructor can ask students to answer questions that require them to communicate their reflections and thought processes.
Students enter your class with different backgrounds and different levels of readiness. You want to help the less prepared students catch up to their peers and be successful, but there isn’t time to provide individual help for all those students. And that is before you even think about the more advanced students, who you would like to keep challenged and to encourage their abilities and interest in the subject. But a good repository of ready-made interactive content, covering different topics and levels, means students with different needs have access to materials that will help them learn on their own. And when that content can be easily customized, you can use it as a starting point to develop more precisely targeted resources, for self-study, classroom demonstrations, projects, or whatever you need.
Content and tools to help students using solutions from the Maplesoft Mathematics Suite include:
Send us a sample lesson from your course, and we will show you how the Maplesoft Mathematics Suite brings learning to life!
Our experts can also provide demonstrations, answer questions, and help you determine which product is best for you and your class.
All of the examples used in this whitepaper come from the Maplesoft Mathematics Suite. This family of products offers online, mobile, and desktop math technology that make it extremely easy to explore, visualize, and solve mathematical problems. Each one provides access to the world’s most powerful mathematics engine through an easy-to-use interface that is designed to meet the needs of students at different phases of their education.
The Maplesoft Mathematics Suite helps with courses from high school all the way through to graduate studies, including: