
The limit command in Maple 2019 has been enhanced for the case of limits of quotients of multivariate functions:
Many such limits that could not be determined previously are now computable, including all of the following examples.
Returning ranges instead of undefined in the bivariate case
| > |
| > |
Support for functions containing abs or radicals
| > |
| > |
Why?
| > |
| > |
| > |
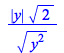 |
| > | ![`assuming`([simplify(`/`(`*`(abs(y), `*`(`^`(2, `/`(1, 2)))), `*`(`^`(`*`(`^`(y, 2)), `/`(1, 2)))))], [real])](MultivariateLimits/MultivariateLimits_14.gif) |
| > | 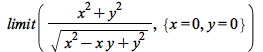 |
| > |
Support for functions in more than 2 variables
| > |
| > |
| > |
Why?
| > |
| > |
| > |
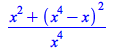 |
| > | 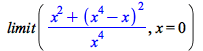 |
| > | 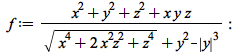 |
| > |
Why?
| > |
| > |  |
| > |
Why?
| > |
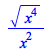 |
| > | ![`assuming`([simplify(`/`(`*`(`^`(`*`(`^`(x, 4)), `/`(1, 2))), `*`(`^`(x, 2))))], [real])](MultivariateLimits/MultivariateLimits_43.gif) |
| > |
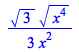 |
| > | ![`assuming`([simplify(`+`(`/`(`*`(`/`(1, 3), `*`(`^`(3, `/`(1, 2)), `*`(`^`(`*`(`^`(x, 4)), `/`(1, 2))))), `*`(`^`(x, 2)))))], [real])](MultivariateLimits/MultivariateLimits_47.gif) |
| > | 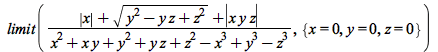 |
| > |
| > |
Why?
| > |
| > |
| > |