Symbolic Math in Mathcad® vs Maple

Both Mathcad and Maple have their own unique design principles. However, Maple’s symbolic math engine is far more powerful, and is allied with an easy-to-use interface.

Here, we describe a few applications of symbolic math in Maple. These are applications for which Mathcad fails to give answers, or simply does not have the functionality to even attempt the analysis.

See more: How does Maple compare with Mathcad?

ODE Solving

Maple offers the world’s most powerful differential equation solvers.

Here, we solve the Euler-Bernoulli equation – a 4th order differential equation - for modeling the bending of a beam.

Euler-Bernoulli equation

$de ≔ EI \cdot \frac{{&DifferentialD;}^{4}}{&DifferentialD; x^{4}} w (x) = q (x) &colon;$

Initial and boundary conditions

$ibc ≔ w (0) = 0, w (L) = 0, (D @@ 2) (w) (0) = 0, (D @@ 2) (w) (L) = 0 &colon;$

Distributed load and point load

$q ≔ x \to Q \cdot (1 - Heaviside (x - a)) + F \cdot Dirac (x - b) &colon;$

Solve the differential equation for beam deflection

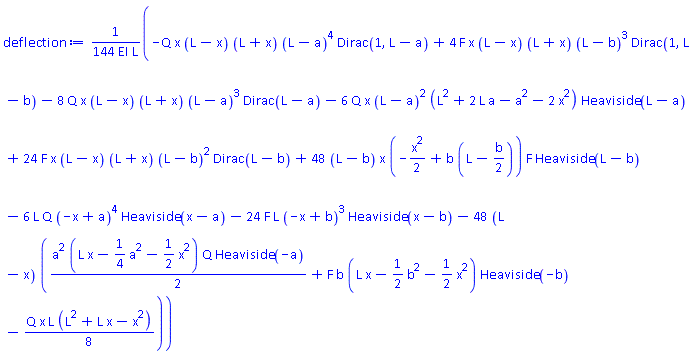
$deSol ≔ dsolve (\{de, ibc\}, w (x)) &colon; deflection ≔ simplify (rhs (deSol), symbolic)$

Mathcad does not offer any tools for solving ODEs symbolically.

PDE Solving

Independent benchmarks show that Maple is the world’s best tool for solving PDEs.

Here, we solve the heat equation. The answer is in terms of the error function, erf.

$pde ≔ \frac{\partial}{\partial t} u (x, t) + 1 = μ \frac{\partial^{2}}{\partial^{} x^{2}} u (x, t) &colon; iv ≔ u (x, 1) = {\begin{array}{c} 0 & x \geq 1 \\ 1 & x < 1 \end{array} &colon; pdsolve ([pde, iv]) assuming μ > 0, t > 0$

$u (x, t) = \frac{3}{2} - \frac{\erf (\frac{- 1 + x}{2 \sqrt{μ} \sqrt{t - 1}})}{2} - t$

Mathcad offers no tools for solving PDEs symbolically.

Solve Equations

Maple has the most powerful symbolic solvers of any math system – here’s why:

Special functions

For example, Maple has a broad database of special functions. These are normally only encountered in advanced mathematical analysis; a few examples are LambertW, Fresnel, Bessel and Appell. Maple lets you use these special functions without any specific training; this helps you rearrange and solve equations that are not possible in Mathcad.

Here, we rearrange the photovoltatic diode equation for the forward current – the result employs the LambertW function.

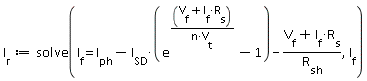
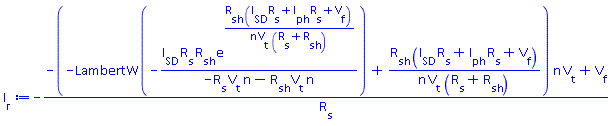
Mathcad only.

Rearrange complicated trigonometric relationships

Modeling the kinematics of a multibody system often results in complicated trigonometric relationships. Deriving the position constraints means you need to rearrange these equations to give the joint angles. This is a tough problem, especially for more complex systems.

Next, we solve for the position constraints of a 2-DOF robot arm to give the joint angles.

$posCons ≔ [\begin{array}{c} \cos (θ_{1}) Tx + \sin (θ_{2}) + \sin (θ_{1}) Ty \\ - \sin (θ_{1}) Tx - 1 - \cos (θ_{2}) + \cos (θ_{1}) Ty \end{array}] &colon; sol ≔ solve (\{{posCons}_{1}, {posCons}_{2}\}, \{θ_{1}, θ_{2}\}, explicit)$

$sol ≔ \{θ_{1} = \arctan (\frac{- {Tx}^{2} - {Ty}^{2} + \frac{({Tx}^{2} Ty + {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}}) Ty}{{Tx}^{2} + {Ty}^{2}}}{Tx}, \frac{{Tx}^{2} Ty + {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}}}{{Tx}^{2} + {Ty}^{2}}), θ_{2} = \arctan (\frac{(- 2 {Tx}^{2} - 2 {Ty}^{2}) ({Tx}^{2} Ty + {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}})}{4 Tx ({Tx}^{2} + {Ty}^{2})} + \frac{{Tx}^{2} Ty + {Ty}^{3}}{2 Tx}, \frac{{Tx}^{2}}{2} + \frac{{Ty}^{2}}{2} - 1)\}, \{θ_{1} = \arctan (\frac{- {Tx}^{2} - {Ty}^{2} - \frac{(- {Tx}^{2} Ty - {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}}) Ty}{{Tx}^{2} + {Ty}^{2}}}{2 Tx}, - \frac{- {Tx}^{2} Ty - {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}}}{2 ({Tx}^{2} + {Ty}^{2})}), = \arctan (- \frac{(- 2 {Tx}^{2} - 2 {Ty}^{2}) (- {Tx}^{2} Ty - {Ty}^{3} + \sqrt{- {Tx}^{6} - 2 {Tx}^{4} {Ty}^{2} - {Tx}^{2} {Ty}^{4} + 4 {Tx}^{4} + 4 {Tx}^{2} {Ty}^{2}})}{4 Tx ({Tx}^{2} + {Ty}^{2})} + \frac{{Tx}^{2} Ty + {Ty}^{3}}{2 Tx}, \frac{{Tx}^{2}}{2} + \frac{{Ty}^{2}}{2} - 1)\}$

Mathcad will not rearrange these equations symbolically.

Control Systems Design

Maple offers tools for symbolic control systems modeling. Here, we find the symbolic controllability matrix for a dc motor described by two differential equations.

$eq_sym ≔ L \cdot \overset{&period;}{i} (t) + R \cdot i (t) = v (t) - K \cdot \overset{&period;}{θ} (t), J \cdot \overset{..}{θ} (t) + b \cdot \overset{&period;}{θ} (t) + Ks \cdot θ (t) = K \cdot i (t) &colon; sys_sym ≔ DynamicSystems :- StateSpace ([eq_sym], inputvariable = [v (t)], outputvariable = [θ (t), i (t)]) &colon; DynamicSystems :- ControllabilityMatrix (sys_sym)$

$[\begin{array}{c} \frac{1}{L} & - \frac{R}{L^{2}} & \frac{R^{2}}{L^{3}} - \frac{K^{2}}{L^{2} J} \\ 0 & 0 & \frac{K}{J L} \\ 0 & \frac{K}{J L} & - \frac{K R}{J L^{2}} - \frac{b K}{J^{2} L} \end{array}]$

Mathcad offers no tools for symbolic control systems design.

Code Generation

Maple can generate C code from symbolic math results. Maple factors out common subexpressions; this makes the code far more numerically efficient than hand-written code.

t1 = Tx * Tx;
t2 = Ty * Ty;

t5 = t1 * t1;
t9 = t2 * t2;
t15 = sqrt(0.4e1 * t2 * t1 - t5 * t1 - t9 * t1 - 0.2e1 * t2 * t5 + 0.4e1 * t5);
t16 = Ty * t1 + t2 * Ty + t15;
t19 = 0.1e1 / (t1 + t2);
t25 = atan2(0.1e1 / Tx * (t19 * Ty * t16 - t1 - t2), t19 * t16);

Mathcad has no code translation tools.

Ready for the next step?

Download a free trial of Maple today.

How to Buy/Licensing Options:

Single User Licenses

Multi-User Licenses

Upgrade to Maple 2024

Maple

Maple Add-Ons

Student Success Platform

Improving Retention Rates

MapleSim

MapleSim Add-Ons

Systems Engineering

Consulting Services

Maple T.A. and Möbius

Education

Industries

Automotive and Aerospace

Robotics

Machine Design & Industrial Automation

Other

Application Areas

Product Pricing

Purchasing

Institutional Student Licensing

Maplesoft Elite Maintenance (EMP)

Support

Product Training

Online Product Help

Webinars & Events

Publications

Content Hubs

Examples & Applications

Community

About Maplesoft

Media Center

User Community

Contact

Maple

ODE Solving

PDE Solving

Solve Equations

Special functions

Rearrange complicated trigonometric relationships

Control Systems Design

Code Generation

Maple

Powerful math software that is easy to use

Maple Add-Ons

Student Success Platform

Improving Retention Rates

MapleSim

Advanced System Level Modeling

MapleSim Add-Ons

Systems Engineering

Consulting Services

Maple T.A. and Möbius

Education

Industries

Automotive and Aerospace

Robotics

Machine Design & Industrial Automation

Other

Application Areas

Product Pricing

Purchasing

Institutional Student Licensing

Maplesoft Elite Maintenance (EMP)

Support

Product Training

Online Product Help

Webinars & Events

Publications

Content Hubs

Examples & Applications

Community

About Maplesoft

Media Center

User Community

Contact

Maple

ODE Solving

PDE Solving

Solve Equations

Special functions

Rearrange complicated trigonometric relationships

Control Systems Design

Code Generation