- Solve a problem at a click of a button, to get the final answer, verify a result, or perform tedious intermediates steps
- Graph an expression, both 2-D and 3-D plots, and zoom in to explore details
- Pose problems, derive full solutions, write conclusions, perform side calculations, add supporting text, and move items around the canvas
- Control parameters through sliders, and watch results and graphs change instantly
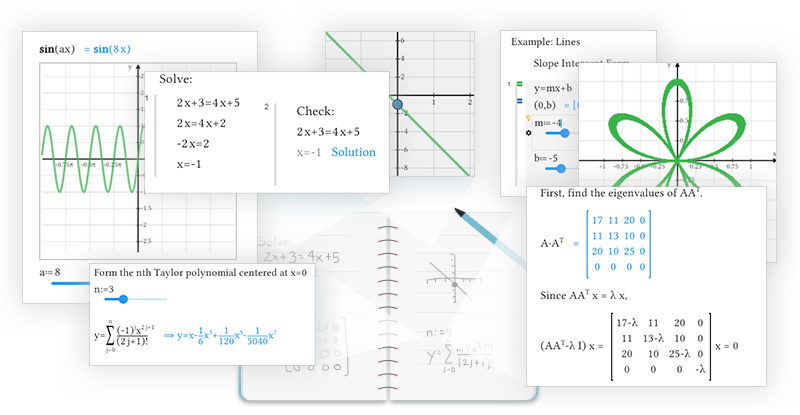
Maple Learn has the Maple math engine behind it, which means it has the mathematical smarts to handle all the math used in math and other courses from high school, two year and technical colleges, and early university. You can use Maple Learn to:
- Calculate formulas
- Solve equations
- Find integrals
- Calculate derivatives
- Invert matrices
- Multiply vectors and matrices
- Row reduce matrices
- Graph expressions
- Factor polynomials
- Simply expressions
- Solve differential equations
- Find medians and means
- Visualize 3-D expressions
- and more!
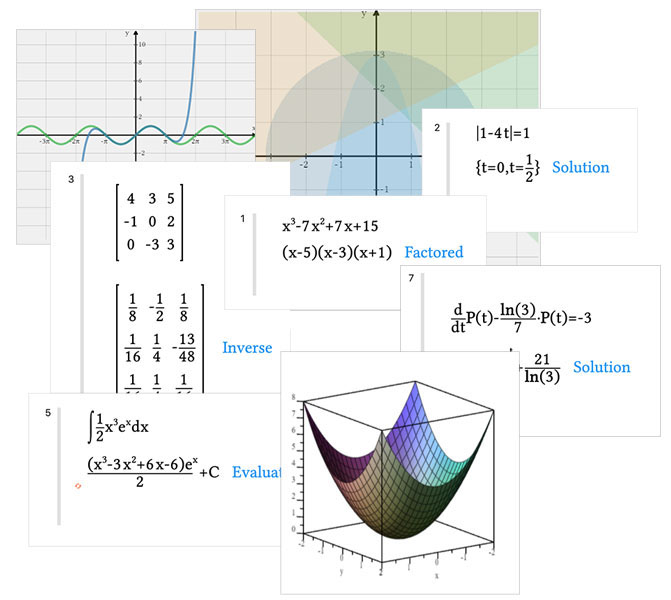
- The rich presentation of textbook content, combining text, math, graphs, and images
- The guided explorations of interactive learning objects that deepen conceptual understanding
- The open-endedness of a notebook where students try things for themselves
In Maple Learn, you can provide your students with lessons, explorations, examples, worked solutions, practise quizzes, homework, and more.
Whether you want to create your own content, or customize some of the thousands of documents already available covering topics in dozens of subjects, Maple Learn is the easiest way to create rich, interactive math-based content and share it with your class online.
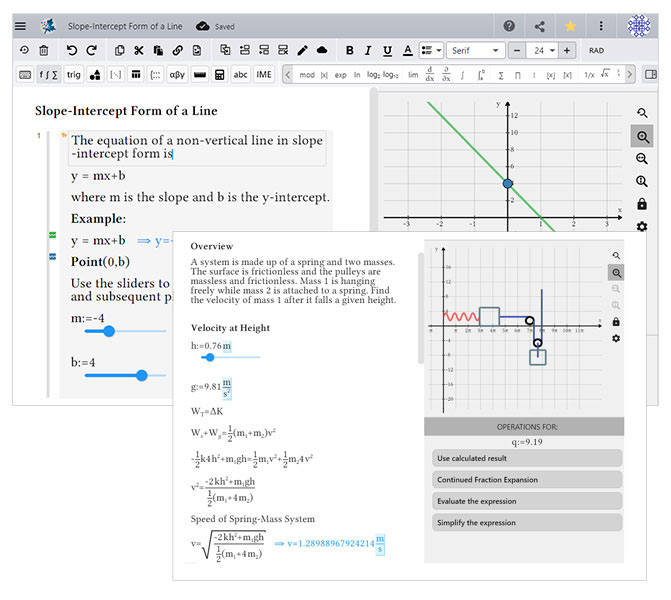






Maple Learn is a versatile math tool that handles math from high school to early university. It is especially suited for teaching and learning:
- Math courses in high school and in two year and technical colleges
- Math courses for non-math majors at university
- Other courses that make frequent use of graphs and calculations, such as economics, business/finance, and physics.
Not what you are doing? Check out the other products in the Maple Math Suite to find the one that best suits your needs.
Maple Learn Classroom is affordable, flexible, and tailored to the needs of your school. It includes:
- Access to Maple Learn for yourself and your students
- Access to thousands of ready-made, customizable examples and applications
- Live one-on-one training with an expert
- Custom-built content designed specifically for your class, created by our content developers