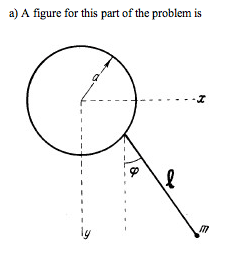
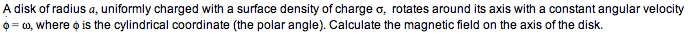Maple has the most comprehensive support for physics of any mathematical software package.
Because of the frequent use of anti-commutative and non-commutative variables, functions, vectors, tensors and matrices; specialized rules and operators; and extremely complex notation, algebraic computations in physics are a serious challenge for most mathematical software. While some specialized systems handle a small fraction of this domain, Maple is the only system that provides the ability to handle a wide range of physics computations as well as pencil-and-paper style input and textbook-quality display of results. In addition, the Physics package is an integral part of the entire Maple system, so using Maple for physics also gives you access to Maple’s full mathematical power, programming language, visualization routines, and document creation tools.
The chart below lists Maple’s capabilities in algebraic computations in physics. In every case, problems in that area can be expressed in Maple using the same notation as you would use when writing the problem on paper, and the results are displayed in the same way as they would be shown in a textbook.
A complete summary of the Physics Package and its commands is also available.