Examples
Example 1.
In this example we shall initialize the Lie algebra 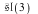 ( the algebra of ( the algebra of 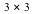 trace-free matrices). For this algebra we then calculate [i] a Cartan subalgebra, [ii] the root space decomposition, [iii] the positive and simple roots, and [iv] the Cartan matrix. trace-free matrices). For this algebra we then calculate [i] a Cartan subalgebra, [ii] the root space decomposition, [iii] the positive and simple roots, and [iv] the Cartan matrix.
| > |
with(DifferentialGeometry): with(LieAlgebras): with(Tensor): with(Tools): |
| > |
LD := SimpleLieAlgebraData("sl(3)", sl3); |
Initialize this algebra.
Calculate a Cartan subalgebra.
| sl3 > |
CSA := CartanSubalgebra(sl3); |
Find the root space decomposition for this algebra.
| sl3 > |
RSD := RootSpaceDecomposition(CSA); |
Find the positive roots and the simple roots.
| sl3 > |
Rts:= LieAlgebraRoots(RSD); |
| sl3 > |
PosRts := PositiveRoots(Rts, [<1,0>, <0, 1>]); |
| sl3 > |
Delta := SimpleRoots(PosRts); |
Find the Cartan matrix.
| sl3 > |
CartanMatrix(Delta, RSD); |
Example 2.
A space-time is called an electro-vac spacetime if there exists an electromagnetic field which solves the Einstein-Maxwell field equations. The problem of deciding if a spacetime is electro-vac can be solved using the command RainichConditions and RainichElectromagneticField.
| M > |
DGsetup([t, x, y, z], M); |
| M > |
g := evalDG(4/3*t^2* dx &t dx + t*(exp(-2*x)* dy &t dy + exp(2*x)*dz &t dz) - dt &t dt); |
Test to see if the Rainich conditions for this spacetime hold.
| M > |
RainichConditions(g); |
We conclude the spacetime is an electro-vac spacetime. Here is the electro-magnetic field.
| M > |
F := RainichElectromagneticField(g); |
| M > |
F := simplify(F) assuming t > 0 |
We check that the Einstein equations are satisfied.
| M > |
T := EnergyMomentumTensor("Electromagnetic", g, F); |
| M > |
E := EinsteinTensor(g); |
We check that the Maxwell equations
are satisfied.
| M > |
MatterFieldEquations("Electromagnetic", g, F); |
Example 3.
The DifferentialGeometry package now supports extended functionality for working with abstract differential forms.
Create an abstract manifold 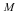 with a function with a function 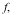 1-forms 1-forms 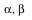 and a 2-form and a 2-form 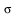 . .
| > |
DGsetup('[f = dgform(0) , alpha = dgform(1), beta = dgform(1), sigma = dgform(2)]', [], M); |
The command DGinfo gives the names of all scalars and forms which are defined.
| M > |
DGinfo("AbstractForms"); |
Scalar products, wedge products and sums of abstract forms can be defined.
| M > |
omega := evalDG(2*alpha &wedge beta + 4*sigma); |
The command DGinfo can also be used to extract information about the form 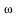 . .
| M > |
DGinfo(omega, "ObjectFrame"); |
| M > |
DGinfo(omega, "FormDegree"); |
| M > |
DGinfo(omega, "CoefficientSet"); |
| M > |
DGinfo(omega , "CoefficientList", [sigma]); |
New forms can be defined on M.
| M > |
DGsetup(M, [delta = dgform(3)],[]); |
| M > |
DGinfo("AbstractForms"); |
We can use the DGzip and GetComponents commands with abstract forms.
| M > |
Omega := evalDG([alpha &w beta, sigma]); |
| M > |
zeta := DGzip([3, 5], Omega, "plus"); |
| M > |
GetComponents(zeta, Omega); |
We can take the exterior derivative of a form.
| M > |
rho:= ExteriorDerivative(alpha); |
The 2-form 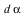 has been added to list of defined forms and is now available for subsequent computations. has been added to list of defined forms and is now available for subsequent computations.
| M > |
DGinfo("AbstractForms"); |
| M > |
ExteriorDerivative(rho); |
Exterior derivatives of defined forms can be specified.
| M > |
DGsetup(M, [], [d(f) = f*alpha, d(beta) = 4*sigma + 5*alpha &wedge beta]); |
| M > |
ExteriorDerivative(f*beta); |
|
